球面稜錐(spherical pyramid)亦稱球角錐，是一種與球有關的幾何體。頂點在球心的稜錐面的一葉在球體上截下的部分，球面被截下的部分稱為球面稜錐的底面。球心稱為球面稜錐的頂點，稜錐面在球內的部分稱為球面稜錐的側面，稜錐的棱在球體內的部分稱為球面稜錐的側棱，顯然，側棱是球體的半徑，側面是球體的大圓扇形，底面為球面多邊形，它是由若干個大圓弧圍成的球面封閉圖形，半徑為R的球的球面稜錐的頂角如果是α球面度，則它的體積是V=αR3/3；底面積是S=αR2。
基本介紹
- 中文名：球面稜錐
- 外文名：spherical pyramid
- 別名：球角錐
- 屬性：一種與球有關的幾何體
基本介紹,相關參數及計算,
基本介紹
球面稜錐(spherical pyramid)亦稱球角錐，是一種與球有關的幾何體。頂點在球心的稜錐面的一葉在球體上截下的部分，球面被截下的部分稱為球面稜錐的底面。球心稱為球面稜錐的頂點，稜錐面在球內的部分稱為球面稜錐的側面，稜錐的棱在球體內的部分稱為球面稜錐的側棱。
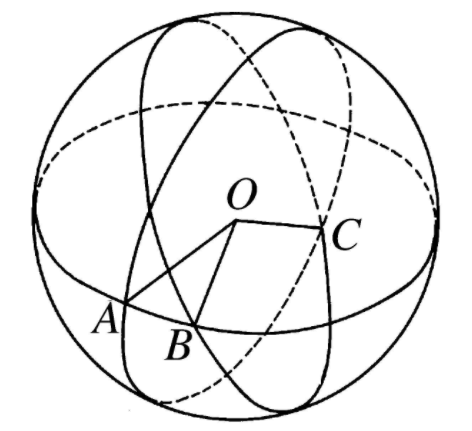圖1相關參數及計算
球面稜錐的側棱是球體的半徑，側面是球體的大圓扇形，底面為球面多邊形，它是由若干個大圓弧圍成的球面封閉圖形，半徑為R的球的球面稜錐的頂角如果是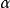
球面度，則它的體積是
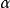
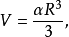
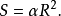
球面稜錐(sphericalpyramid)是由球面多邊形與通過球心和該多邊形的邊的各平面所構成的圖形。其體積等於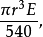
其中
是球的半徑，E是該球面多邊形的球面角盈。
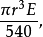
球面上的多邊形內角之和減去與該多邊形具有相同邊數的平面多邊形內角之和，稱為該球面多邊形的球面角盈(spherical excess)。這裡球面多邊形是指球面上一些大圓弧所圍成的圖形。在半徑為1的球面上，球面多邊形的球面角盈等於該多邊形的面積。
