球扇形

一個圓扇形繞著一條不通過它的內部的直徑旋轉一周所得的幾何體，叫做球扇形(spherical sector)，又稱球心角體、球分，圓扇形的弧旋轉所形成的球冠或球帶叫做球扇形的底，這個球冠或球帶的高叫做球扇形的高。設球扇形的高為h，球半徑為R，則球扇形的體積為V=2πR²h/3。

基本介紹

• 中文名：球扇形
• 外文名：spherical sector
• 別稱：球心角體、球分
• 所屬學科：數學
• 所屬問題：立體幾何（球）
• 簡介：一種與球有關的幾何體

基本介紹

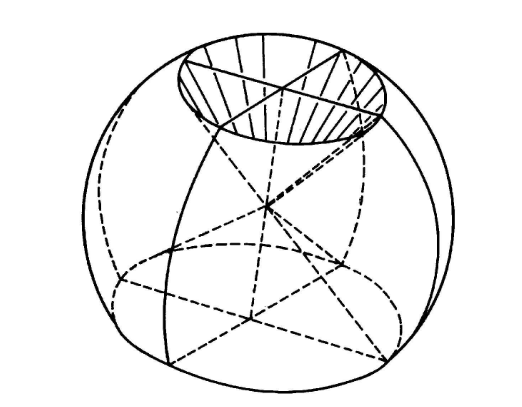圖1

球扇形亦稱球心角體，是一種與球有關的幾何體。它是球的一部分，一個頂點在球心的旋轉圓錐面把球體截成兩部分，每一部分都稱為球扇形，用兩個頂點在球心，共軸而不相等的旋轉圓錐面把球體截成三部分，每一部分也稱為球扇形，將一個不足半圓的圓扇形，繞一條在扇形平面上的過圓心而不穿過扇形內部的直線旋轉，也可生成球扇形。扇形圓弧旋轉所得到的球冠或球帶稱為球扇形的底面，這個球冠或球帶的高稱為球扇形的高，扇面的半徑旋轉生成的圓錐側面稱為球扇形的側面，當旋轉軸與扇形有一直邊重合時，生成的球扇形稱為簡單球扇形，亦稱球面圓錐，否則稱為中空球扇形。

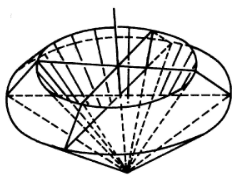圖2

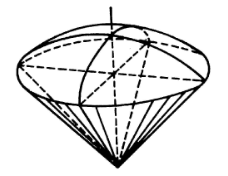圖3

例題解析

【例1】已知1/4圓弧，∠AOB=∠BOC=∠COD，⊙O的半徑為R，求扇形BOC繞直線AO旋轉一周所得的球扇形的表面積。

解 線段OB旋轉成的圓錐面面積

線段OC旋轉成的圓錐面面積

圓弧旋轉成的球帶面積

∴ 所得的球扇形的表面積

【例2】垂直於球直徑的平面截此球面，若截面面積等於所分成的兩個球冠面積之差，試證：大球冠的高是小球冠的高和球直徑的比例中項.當球的半徑為2時，求以小球冠為底的球扇形的底面積.

解 設球半徑為R，大球冠的高為h，截面圓半徑為r，則小球冠的高為(2R-h)，且由直角三角形中的射影定理和勾股定理有r²=h (2R-h)，(h-R)²+r²=R²。

消法r得關係式h²=2R (2R-h)，即大球冠的高是小球冠的高和球的直徑的比例中項。

當R=2時，球扇形的底面積為。