么半群,是指在抽象代數此一數學分支中,么半群是指一個帶有可結合二元運算和單位元的代數結構。
么半群在許多的數學分支中都會出現。在幾何學中,么半群捉取了函式複合的概念。
結合的酉群胚叫么半群。例如,賦以加法(或乘法)的自然數集N是么半群。
基本介紹
- 中文名:么半群
- 外文名:monoid group
- 領域:數學
- 學科:抽象代數
- 性質:代數結構
- 定義:結合的酉群胚
定義,半群,衍生概念,交換么半群,冪關係,子么半群,自然預序,序單位,性質,與商么半群,同態,舉例,作用和運算元,範疇論,
定義
即,考慮定義了二元運算 (注意這裡蘊含了S對運算
(注意這裡蘊含了S對運算 封閉)的非空集合S,若滿足如下公理:
封閉)的非空集合S,若滿足如下公理:


結合律: ,有
,有


單位元: ,使
,使 ,有
,有



則三元組 稱為么半群。
稱為么半群。

半群
最簡單、最自然的一類代數系統。一個非空集合S連同定義在它上面的一個結合的(即滿足結合律的)二元運算“·”的代數系統(S,·)稱為一個半群。半群(S,·)簡記為S。
半群是群的推廣。群自然是半群;反之顯然未必.半群也是環的推廣.環在只考慮它的乘法運算的時候是一個半群,稱為環的乘半群;但任何一個帶零半群卻未必是某個環的乘半群。半群代數理論的系統研究始於20世紀50年代(雖然,這方面的工作可追溯到1904年蘇士凱維奇(Suschkwitz,A.K.)關於有限半群的論文)。在數學內部和外部的巨大推動下,半群理論已成為代數學的一個公認的分支學科,並早已以其特有的方法獨立於群論和環論之外。在20世紀60年代,蘇聯和美國率先出版了兩本專著,利雅平(Ляпин,E.C.)的《半群》和克利福德(Clifford,A.H.)與普雷斯頓(Preston,G.B.)的兩卷《半群代數理論》,這對半群代數理論的發展,在國際上起了巨大的推動作用.由德國斯普林格出版社出版的《半群論壇》更是有關半群理論的一個重要的國際性專門刊物。許多數學家在世界各地開展半群理論的研究和各層次高級人才的培養(直到博士後).半群代數理論是半群理論中最基本、最活躍、也最富成果的一部分.此外,尚有半群的分析、拓撲和序理論。
衍生概念
交換么半群
設 是么半群,若運算
是么半群,若運算 還滿足交換律,則
還滿足交換律,則 稱為交換么半群或阿貝爾(Abel)么半群。交換么半群經常會將運算寫成加號。
稱為交換么半群或阿貝爾(Abel)么半群。交換么半群經常會將運算寫成加號。



冪關係
設 是么半群,對
是么半群,對 可以定義其非負次冪為:
可以定義其非負次冪為: ,
, 以及對
以及對 ,
, (n次自乘)。
(n次自乘)。






子么半群
設 是么半群,考慮其子集M。若
是么半群,考慮其子集M。若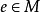 ,且M對運算
,且M對運算 封閉,則易驗證,
封閉,則易驗證, 也是么半群。稱為子么半群。
也是么半群。稱為子么半群。

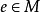


等價地,子么半群是一個子集 N ,其中 N=N ,且上標 * 為克萊尼星號。對任一於 M 內的子集 N 而言,子么半群 N 會是包含著 N 的最小么半群。
子集 N 被稱之為 M 的生成元,若且唯若 M=N。若 N 是有限的, M 即被稱為是有限生成的。
自然預序
設 是交換么半群,可以以如下方式在其上定義自然代數預序 ≤ :
是交換么半群,可以以如下方式在其上定義自然代數預序 ≤ :





序單位
設 是交換么半群,≤是依上述方式定義的自然預序。若
是交換么半群,≤是依上述方式定義的自然預序。若 ,滿足:
,滿足:





則稱u是S的序單位。
序單位經常用在 M 是偏序阿貝爾群G 的正錐體的情況。有接受任何交換么半群,並把它變成全資格阿貝爾群的代數構造;這個構造叫做格羅滕迪克群。
性質
逆元素:一元素x稱為可逆,若存在一元素y,使得x*y = e且y*x = e。此一元素y便稱做x的逆元素。結合律使得其逆元素(若存在)是唯一的。
若 y是x的逆元素,則可以定義x的負冪,以x=y及 x=y*...*y (乘上n次),其中n>1。如此冪的規則在所有整數就都成立了,這也是為什麼x的逆元素通常會寫做x。所有在么半群M內的可逆元素,和其自身的運算可組成一個群。在這意思之下,每個么半群都含有一個群。
但並不是每個么半群都包含在一個群內的。例如,絕對可能有一個么半群,其兩個元素a和b會有a*b=a的關係,即使b不是單位元。如此的么半群是不可能包含於一個群內的, 因為在群里,兩邊一同乘a的逆元素,就會得到b = e的結果,但這不是真的。一個么半群(M,*)若具有消去性,即表示對任何在M內的a、b、c,a*b = a*c永遠意指b = c且b*a = c*a也永遠意指b = c。一具有消去性的可交換么半群總是可以包含於一個群內。這是為什麼整數(加法運算下的群)可以由自然數(具有消去性的加法運算下的可交換么半群)建立。但一具有消去性的不可交換么半群則一定不可能包含於一個群之中。
若一么半群有消去性且是有限的,它會是一個群。
一可逆么半群為一么半群,其任一在M內的a,總存在一唯一在M內的a,使得a=aaa且a=aaa。
一么半群G的子么半群是G的子集H,其包含有單位元,且若x、y屬於H,則xy屬於H。很清楚地,H本身也是個么半群,在G的二元運算之下。
與商么半群
么半群同餘是相容於么半群乘積的等價關係。就是說它是子集
使得它是自反的、對稱的和傳遞的(如同所有等價關係必須的那樣),還要有如果 且 對於所有 M 中的 x,y,u 和 v,則有 的性質。
么半群同餘引發同餘類
而么半群運算 * 引發在同餘類上的二元運算 :
它是么半群同態。它明顯的也是結合的,所以所有同餘類的集合也是么半群。這個么半群叫做商么半群,可以寫為
一些額外的符號是公用的。給定子集 ,寫
對於引發自 L 的同餘類的集合。在這個表示法中,明顯的。但是一般的說, 不是么半群。走相反的方向,如果 是商么半群的子集,寫
當然這只是 X 的成員的並集。一般的說, 不是么半群。
明顯的有 且。
同態
兩個么半群(M,*)和(M′,@)之間的同態是一個函式f : M → M′,會有如下兩個性質:
f(x*y) = f(x)@f(y) 對所有在M內的x和yf(e) = e′ 其中e和e′分別是M和M′的單位元。
不是每一個群胚同態都會是個么半群同態,因為它不一定會維持單位元。和上述不同,群同態的情況則會成立:群論的公理確保每一兩群之間的群胚同態都會維持住單位元。對於么半群,這不是永遠成立的,而必須有另外的要求。
舉例
每一個單元素集合{x}都可給出一個單元素(當然)么半群。對定固的x,其么半群是唯一的,當其么半群公理在此例子必須滿足x*x=x時。
每一個群都是么半群,且每一個阿貝爾群都是可交換么半群。
每一半格都是等冪可交換么半群。
任一個半群S都可以變成么半群,簡單地加上一不在S內的元素e,並定義ee=e和對任一在S內的s,es=s=se。
自然數N是加法及乘法上的可交換么半群。
以加法或乘法為運算,任何單作環的元素
以加法或乘法為運算的整數、有理數、實數及複數
以矩陣加法或矩陣乘法為運算,所有於一環內n×n矩陣所組成的集合
某些固定字母Σ的有限字元串所組成的集合,會是個以字元串串接為運算的么半群。空字元串當成單位元。這個么半群標記為Σ*,並稱為在Σ內的自由么半群。
給定一么半群M,並考慮包含其所有子集的冪集P(M)。這些子集的二元運算可以定義成S*T={s*t:s在S內且t在T內}。這使得P(M)變成了具有單位元{e}的么半群。依同樣的方法,一個群的冪集是一在群子集的乘積下的么半群。
設S為一集合。由所有函式S→S所組成的集合會是在複合函式下的么半群。其單位元為恆等函式。若S為有限的且有n個元素,其么半群也會是有限的,且有nn個元素。
廣義化上述的例子,設C為一範疇且X為C內的一對象。由X所有自同態組成的集合,標記為EndC(X),是一在態射複合下的么半群。更多有關範疇論和么半群的關係請見下述。
在連通和下的閉流形同態類所組成的集合,其單位元為一般二維球面類。此外,當a標記為環面類且b標記為射影平面類,此一么半群的每一個元素c都會有一唯一的表示式c=na+mb,其中n是大於等於零的整數,m為0、1或2,且會有3b=a+b。
設<f>;是一個數為n的循環么半群,亦即<f>={f0,f1,..,fn−1}。然後,fn=fk,其中。事實上,不同的k會給出不同的么半群,且每個么半群都會和另一個同構。
注意當k=0時,函式f是{0,1,2,..,n−1}的置換,並給出個數為n的唯一循環群。
作用和運算元
主條目:么半群作用
運算元么半群是一作用在集合X上的么半群M。亦即,存在一運算$:M×X→X符合么半群的運算。
對任一在X內的x:e$x=x。
對任何在M內的a、b及在X內的x:a$(b$x)=(a*b)$x。)=(a*b)·x.
運運算元么半群也叫做作用(因為它們類似於群作用),轉移系統,半自動機或變換半群。
範疇論
么半群可視之為一類特殊的範疇。么半群運算滿足的公理同於範疇中從一個對象到自身的態射。換言之:
么半群實質上是只有單個對象的範疇。
精確地說,給定一個么半群(M,*),可構造一個只有單個對象的小範疇,使得其態射由M的元素給出,而其合成則由么半群的運算*給出。
同理,么半群之間的同態不外是這些範疇間的函子。就此意義來說,範疇論可視為是么半群概念的延伸。許多關於么半群的定義及定理皆可推廣至小範疇。
么半群一如其它代數結構,本身也形成一個範疇,記作Mon,其對象是么半群而態射是么半群的同態。
範疇論中也有么半對象的概念,它抽象地定義了何謂一個範疇中的么半群。

