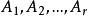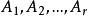簡介
狄利克雷過程(Dirichlet Process, DP)是一個隨機過程,其樣本軌道是機率測度。從DP中抽取樣本可以理解成抽取隨機分布。它在非參數貝葉斯模型中有廣泛運用,最常見的套用是作為Dirichlet過程混合模型(Dirichlet Process Mixture Model, DPMM,也叫做無限混合模型,infinite mixture model)的先驗。它被稱為Dirichlet過程是因為它在有限維上的邊緣分布是Dirichlet分布。像高斯過程一樣(這是另一個有名的隨機過程,用在貝葉斯回歸中,可參考機器學習中的高斯過程),它的有限維邊緣分布是高斯分布。從Dirichlet過程中抽取的分布是離散的,但無法使用有限個參數描述,因此它被歸為非參數模型。
定義
對於一個隨機分布G,如果他是基於DP的分布,那么它的邊緣分布就是Dirichlet分布。特別的,假設H是基於參數
的分布,
是一個正的實數值。那么,對於參數
任意有限測度劃分
,它都是隨機的。
我們說G是基分布為H,集中參數為
的狄利克雷過程,記作
,當有如下情況時:
套用
狄利克雷過程可以用來估計密度函式、聚類、構造層次狄利克雷過程等。同時,它也常常作為狄利克雷混合模型的先驗。