特里科米問題

簡介

一偏微分方程在所考慮的區域的某一部分上是橢圓型的,在另一部分上是雙曲型的,這些部分由一些曲線(或一些曲面)所分隔，在分界線(面)上方程或者退化為拋物型的,或者是不定義的,這樣的方程稱作混合型方程。

對此方程特里科米提出了一種新的邊值問題，也就是特里科米問題。特里科米問題(Tricomi problem)最早系統研究過的混合型偏微分方程的邊值問題。對最簡單的線性混合型方程(也稱為特里科米方程)。

特里科米(Tricomi , F. G.)在如下的邊界條件下建立了解的存在性和惟一性定理:設AC,BC是方程在雙曲區域中的特徵線，是連結A,B在橢圓區域中的若爾當曲線，它們圍成區域D，在AC(或 BC)及。上給定邊值.這種邊值問題稱為特里科米問題。恰普雷根方程的特里科米問題也有意義。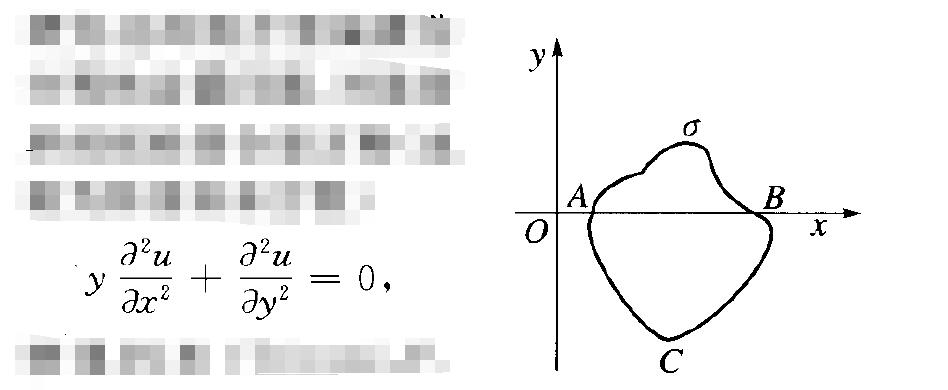

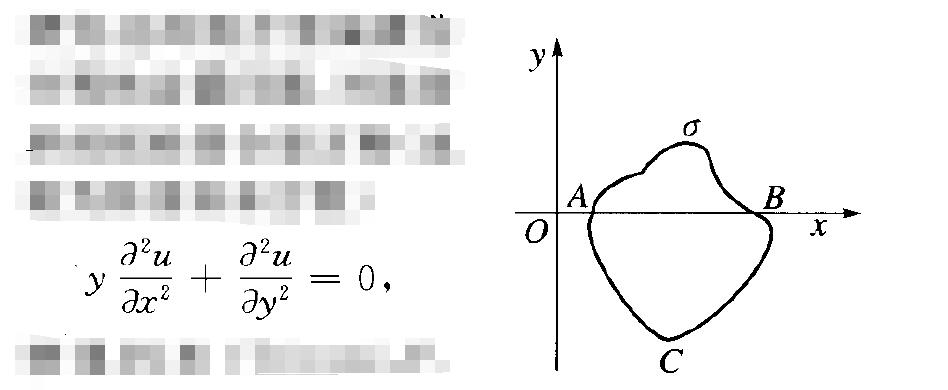
特里科米通過解奇異積分方程問題證明了這個問題解的存在性。自特里科米的工作之後，混合型方程，特別由於它與跨音速、超音速流動理論有著直接聯繫而引起了廣泛的重視，從40年代起不斷有人對它進行研究，基本上在三個方面開展工作：①提出新的邊值問題，並證明解的存在性和惟一性；②尋求新的研究工具和途徑，且不斷減弱在證明可解性時所附加在方程係數和邊界曲線上的限制；③利用混合型方程解決氣體動力學、幾何學和彈塑性力學中的各種問題。

發展史

混合型方程的研究歷史比較短。1923年，義大利F.G.特里科米最先研究了方程

。

美國數學家K.O.弗里德里希斯在50年代末建立了正對稱方程組的理論，在一定意義下統一地處理雙曲、拋物、橢圓以及混合型方程的邊值問題。將此理論套用於混合型方程的研究，不僅得到了一些適定的新的邊值問題，而且也提供了新的研究工具：能量不等式、強弱解一致性和解的可微性等。同時還促進了多個自變數的和非線性的混合型方程的研究。混合型方程的研究還與彈性薄殼無旋理論、幾何曲面變形理論以及其他物理、力學問題等有著廣泛的聯繫。
除上述那種方程外，還有一類方程(方程組)，它們是在域的某些點集(包括邊界點)上發生型的蛻化，但在區域上並不同時出現有橢圓型和雙曲型。這類方程(組)被稱為退化方程（組）。退化方程（組）可分為退化拋物型方程、退化橢圓型方程（二者合在一起還稱為具有非負特徵的方程）、退化雙曲型方程（組）等。退化方程（組）在邊界層理論、無旋薄殼理論、滲流理論、擴散過程理論及其他許多物理和力學問題中遇到。混合型方程的研究更促進了對退化橢圓型方程和退化雙曲型方程的深入研究。這類方程（方程組）基本上在兩個緊密聯繫的方向上開展研究：

①證明邊值問題的可解性，在此考慮到由於型的蛻化而在問題提法上的改變；

②研究解的性質，特別是建立類似於非退化方程的解的性質。

特里科米問題

基本介紹

簡介

發展史

相關詞條

熱門詞條