特徵價格法,又稱Hedonic模型法和效用估價法,認為房地產由眾多不同的特徵組成,而房地產價格是由所有特徵帶給人們的效用決定的。由於各特徵的數量及組合方式不同,使得房地產的價格產生差異。因此,如能將房地產的價格影響因素分解,求出各影響因素所隱含的價格,在控制地產的特徵(或品質)數量固定不變時,就能將房地產價格變動的品質因素拆離,以反映純粹價格的變化。
基本介紹
- 中文名:特徵價格法
- 別名:Hedonic模型法、效用估價法
理論基礎
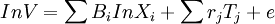
優缺點
主要形式
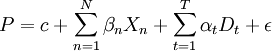
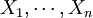
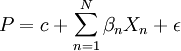
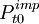
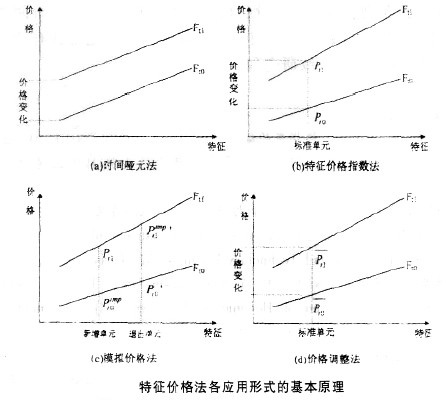

特徵價格法,又稱Hedonic模型法和效用估價法,認為房地產由眾多不同的特徵組成,而房地產價格是由所有特徵帶給人們的效用決定的。由於各特徵的數量及組合方式不同,使得房地產的價格產生差異。因此,如能將房地產的價格影響因素分解,求出各影響因素所隱含的價格,在控制地產的特徵(或品質)數量固定不變時,就能將房地產價格變動的品質因素拆離,以反映純粹價格的變化。
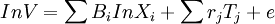
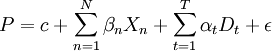
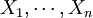
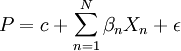
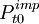

特徵價格法,又稱Hedonic模型法和效用估價法,認為房地產由眾多不同的特徵組成,而房地產價格是由所有特徵帶給人們的效用決定的。由於各特徵的數量及組合方式不同,使得房地產的價格產生差異。因此,如能將房地產的價格影響因素分...
第二節 主要房地產價格指數編制方法述評 一、簡單方法述評 二、加權方法述評 三、重複交易法述評 四、特徵價格法述評 五、混合模型法述評 第三節 主要房地產價格指數編制實踐述評 一、國外典型房地產價格指數介紹 二、國內現行的主要房地產價格指數述評 三、現行房地產價格指數編制實踐的局限性 第四節 特徵價格法應...
特徵價格法 (Hedonic Price Method) 特徵價格法,又稱Hedonic模型法和效用估價法,認為房地產由眾多不同的特徵組成,而房地產價格是由所有特徵帶給人們的效用決定的。由於各特徵的數量及組合方式不同,使得房地產的價格產生差異。因此,如能將房地產的價格影響因素分解,求出各影響因素所隱含的價格,在控制地產的特徵(...
價格串通行為最突出的特徵是破壞競爭,其目的是迴避競爭對定價行為的約束,其違法後果是直接擾亂了市場競爭秩序。根據《價格法》第十四條規定,認定經營者存在價格串通行為,需要把握以下幾個要件:(一)兩個以上經營者相互串通 價格串通作為一種多方行為,經營者一定是複數。從實際案例看,參與串通的經營者少則兩三家...
依據《中華人民共和國價格管理條例》、《中華人民共和國價格法》、《中華人民共和國行政處罰法》和《價格違法行為行政處罰規定》等相關規定執法。特徵 價格監督檢查屬於行政監督檢查的一種。其特徵有:1.價格監督檢查的主體是政府價格主管部門。2.價格監督檢查的對象是價格管理相對人,包括公民、法人、其他組織和國家機關...
(一)以價格違法行為的表現形式為標準,價格違法行為可以分為以下兩種類型:一是作為的價格違法行為。是指價格管理相對人積極主動地實施價格法律規範所禁止的行為而構成的價格違法行為。如《價格法》第十四條規定的行為:屬於作為的價格違法行為。二是不作為的價格違法行為。是指價格管理相對人消極被動地實施價格法律規範...
1.價格法規、規章與《價格法》不一致,導致立法之間的衝突。如《價格法》規定:“政府指導價,是指依照本法規定,由政府價格主管部門或者其他有關部門,按照定價許可權和範圍規定基準價及其浮動幅度,指導經營者制定的價格。 ”但《某省物業管理條例》卻規定:“政府指導價由省人民政府價格行政主管部門會同建設行政主管...
當參照物與評估對象的差異僅僅體現在某一種基本特徵上的時候,直接比較法還可能演變成以下具體的評估方法,如現行市場法、市價折扣法、功能價值類比法、價格指數法和成新率價格調整法等。如果當參照物與評估對象的差異不僅僅體現在某一基本特徵上的時候,上述評估方法的運用就可以演變成參照物與評估對象各個基本特徵修正...
