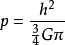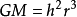“牛頓宇宙”是一個絕對的、精確的世界,所有物質、整個宇宙都由各種客觀存在的粒子構成,不論過去、現在和未來,時間都以固定的速度流逝;因果關係就像上帝的戒律一樣嚴格,絕無例外,未來可以完全由過去來預測。
基本介紹
- 中文名:牛頓宇宙
- 性質:絕對的、精確的世界
- 構成:各種客觀存在的粒子構成
- 屬於:牛頓宇宙學
宇宙原理,主要特點,宇宙年齡,
宇宙原理
1、我看到的宇宙
我處於一個大大的真空中,周圍的光子直線光速向我飛來,那么同時到達我處的光子必定處於半徑為r的球面上,有c=hr,h是球面光子到達我所需時間的倒數。設兩個光子所走直線的來角為θ,那s=rθ是兩個光子在球面上的弧線距離。那么ds/dt=cθ,即在這兩個光子的歷史中,其弧線距離的速度是一個正比於θ的勻速。
當θ=0時,兩個光子相對靜止,θ為定值時兩個光子相互勻速弧線運動,當θ變化時兩個光子相互弧線加速運動。
c=hr,是雙曲線圖形,當r極大時,h是一個極小的常數,如同哈勃膨脹。當h極大時,r是一個極小的常數,如同微觀粒子。即我在近處看到微觀粒子,在遠處看到宇宙的膨脹。
2、力學分析
力是同時性物體之間的,球面上的兩個光子之間如果存在力,只能是弧線性傳遞,方向是孤線的切線。如果質量為M和m的光子存在引力則f=GmM/s2,當θ不變時光子合力為零,那么有力F=mh2s 反向等於f,同時F=Mh2s,推導出θ不變的兩個光子質量相等,且它們在半徑為s的球中分布密度為正比於h的平方的常數。我將M與m改稱為物量以區別於一般意義的質量,物量密度在一定空間內密度為常數的性質,簡稱為物密守恆定律。
3、光子的球面動能
F=mh2s,dw=Fds,則W=mh2s2/2.有v=hs,則有W=mv2/2,E=2W=mv2,當v=c時,得出質能關係式E=mc2
4、物量分布
GM=h2s3=c2rθ3,當θ為定值時,物量正比於r,也正比於s,即兩個光子離的越近其空間內含的物量越小,反之則越大。θ的最大值為1,那么在r的距離內的光子對所含的最大物量是
M=c2r/G
在光子半徑為r的範圍內,若進入物質,則半徑變大,或者反射或透射稱為輻射物質,或者半徑變大的同時輻射出部分物質以維持物量密度守恆。若輻射物質則半徑變小。
原子應是物量密度守恆的模型。原子可以視為光子的集合。
5、暗物質
彼此夾角大於1的光子互為暗物質。
如果我是一個光子,那么暗物質就在我的周圍,從距離為零一直到距離無窮大的空間記憶體在的暗物質遠遠多於看得見的物質。
6、光速不變的原因
當θ=1時,兩個光子以光速分離,當r極大時,無論光子的相互運動有多快,對於θ的影響都可以忽略不計,因此光速不變。
光子在介質中速度變慢的原因,因為光子進入原子半徑時,由乾物密守恆定律,原子半徑變大吸收了光子的能量,所以光子變慢了。
7、波長的含義
λ波長的光,相當於距我r=λ,c=λf,那么h=f
由於光子是不加速的,那么光子到達我處所做的功是零。而光子的質量也為零,那么光子的能量怎么體現呢?
波長越短頻率越高,如果每個光子的能量相等,那么頻率代表的是單位時間內到達我處的光子數,我所能接收的光子的能量正比於光子的頻率。根據物密守恆定律半徑為λ的球體內物量是有限的,那么光子面的總能量正比於光子的頻率,這就是普朗克公式,E=нf
所謂光量子就是距離我半徑為λ的球面上射入我處的單位時內最大的光子數的總和。
我所能接待的光子是有限的而不是無限的。如果我也遵守物密守恆定律,那么我也一定會送
走一波客人,再接待另一波客人,在客滿的情況下。
頻率越高波長越長,客人就越多,我的小院只能容納多少客人是一定的。從我院門進入的客人數是由門決定的,而不是客人的多少決定的。
8、光的波動性
光子在球面上存在兩個互相重直的振動,這個振動方向是隨機的,是由球面上光子的互相吸引和排斥的分布情況決定,在直線運動的光線中,其中心點一直處於直線中。
兩個光子離我越近,它們的s越小,h越大,如果物量是個確定值的化,它們之間的吸引力將使它們靠在一起,顯然不合理想,因為我在第一章中已暗示光子不受力或合力為零,所以,物量是可變的,而不是絕對的質量,物量密度是守恆的,所以兩個光子靠得近就有一個力使它分得開,這個動態的過程就是波動。
這個波動的頻率是怎么確定的呢?
這個頻率f=h,v=ds/dt=θdr/dt=θhr=hs=fs,所以f=h
9、物量與質量
在特定的空間中,兩個光子之間的物量是一個確定值,把這個值作為一個單位,那么在一個較大的空間中含有單位物量的多少就是這個空間所含的質量。質量總是小於空間所能含有的物量,質量越小,空間越空虛。
物體是物量的集合,它們之間的引力與物量一樣滿足反平方律。物體隔著虛空沒有相互作用,因此物體各有各的質量。
主要特點
牛頓宇宙學
<BLOCKQUOTE>因為天體運動在很大尺度範圍速度遠小於真空中光速,牛頓力學亦能很好地說明宇宙圖象。最後為定性半定量地聯繫個別近代宇宙學問題,會用到狹義相對論的少量知識,但全文均不考慮廣義相對論效應。
在夏日晴朗的夜晚,抬頭遙望天空,看到銀河系中的星星分布得相當稀疏。據天文觀察,類似銀河得星系有許許多多,它們在宇宙太空中得分布也很稀疏。但在更大得空間範圍內去統計星系物質的分布,卻發現星係數密度和質量密度幾乎是相同的。宇宙是如此巨大,上述大空間範圍在宇觀上竟可以近似處理為一個點!然而,事實確是如此。這樣,在討論宇宙學問題時,可以把宇宙空間處理為由這樣的宇宙點構成的連續空間,宇宙中的物質也同樣處理為連續分布。
宇宙運動學
宇宙運動學依據的一條原理,即為哥白尼原理:在宇宙中沒有特殊位置,每一個位置的靜止觀察者朝任一個方向看到的宇觀現象都是一樣的。
由這一原理,可以得出宇宙的若干性質。
在宇宙中任一點觀察,宇宙均為中心對稱。
由於不存在特殊位置,亦不存在特殊方向,故宇宙有旋轉對稱性,即具有中心對稱性。
同一時刻測量宇宙各點,密度均相等。
如圖1所示,O處測量者測得O`處密度為ρ(r),因宇宙相對O具有中心對稱,因此ρ(r)=ρ(r)
O`處測量者測得O處密度ρ(r`)也具有中心對稱性質,ρ(r`)=ρ(r`),
因宇宙中沒有特殊位置,因此ρ(r)=ρ(r`),或者ρ(r)=ρ(r`)
宇宙中任一點對其它質點進行測量的關係
宇宙中任一點觀察者對其它點地物質或者說質點進行測量,後者相對於前者地速度v與前者到後者地矢徑r間滿足關係式
v=αr
其中α是一個僅與時間有關地量。
首先由宇宙地中心對稱可知,任何兩點之間地相對速度v必定沿兩點連線方向r,即有v=αr。如圖2所示,取O、O`、P三點。P相對於O的速度記為v<SUB>r</SUB>;,P相對於O'的速度記為v<SUB>r'</SUB>;,O'相對於O的速度記為v<SUB>e</SUB>;,相應的位矢也在圖中示出。所有測量均在同一時刻實現,速度間滿足經典疊加關係,即有
v<SUB>r</SUB>=v<SUB>e</SUB>+v<SUB>r'</SUB>
又由v=αr,可得v<SUB>r</SUB>=αrr,v<SUB>r'</SUB>=α<SUB>r'</SUB>r',v<SUB>e</SUB>=α<SUB>e</SUB>r<SUB>e</SUB>
而由圖中相似三角形關係,可得
即得 α<SUB>r</SUB>=α<SUB>r'</SUB>=αe
可見對任一觀察者,α為相同的量,此量與觀察者的位置無關,與被觀察者的位置無關,但可以與測量時刻t有關。
宇宙動力學
運動學所描述的是一個瞬時宇宙圖景,為對動態宇宙有所了解,須從動力學方面考慮。
如圖3所示,設t時刻距觀察者O為r處的質點P具有速度v,應有v=α(t)r
在t=t<SUB>0</SUB>;時刻有v<SUB>0</SUB>=α(t<SUB>0</SUB>)r<SUB>0</SUB>
引人參量 H<SUB>0</SUB>=α(t<SUB>0</SUB>)
則有 v<SUB>0</SUB>=h<SUB>0</SUB>r<SUB>0</SUB>
在以O為球心、r(t)為半徑的球體內,取任意一點Q,Q相對O的位矢r'(t)<r(t),速度為v',則有v'=α(t)r',v'<v,即在以後任意時刻Q的速度恆小於P的速度,這表明Q點永遠不會運動到以O為球心、P點所在球面之外,據此可知,P點所在球面內的質量守恆。
再設t時刻宇宙各處密度為ρ(t),t=t<SUB>0</SUB>;時刻的密度記為ρ<SUB>0</SUB>;。ρ(t)及P點到O點的距離r均會隨t而變化,但有質量守恆可得 ρr<SUP>3</SUP>=ρ<SUB>0</SUB>r<SUP>3</SUP>
由於宇宙物質相對O點具有球對稱分布,以P所在球面為界,球面外物質對P的萬有引力合力為零,球面內物質對P的萬有引力相當於一個質量恆定的球體對外部質點的萬有引力。據此,P質點的引力勢能為E<SUB>P</SUB>=-GMm/r其中m為P的質量,M為球體總質量,r為O點到P點的距離,M可表述為 M=4πr<SUP>3</SUP>;ρ/3=4πr<SUP>3</SUP><SUB>0</SUB>;ρ<SUB>0</SUB>/3
P質點的機械能為E=E<SUB>K</SUB>+E<SUB>P</SUB>=mv<SUP>2</SUP>/2-GMm/r=mv<SUP>2</SUP>/2-4πGmr<SUP>3</SUP><SUB>0</SUB>;ρ<SUB>0</SUB>/(3r)
機械能守恆要求E=E<SUB>0</SUB>;(常量)。引人一個新的常量 K=2E<SUB>0</SUB>/mr<SUB>0</SUB><SUP>2</SUP>
則機械能守恆可表示為 K=v<SUP>2</SUP>/r<SUB>0</SUB>2-8πr<SUB>0</SUB>;ρ<SUB>0</SUB>/(3r)
由t=t<SUB>0</SUB>;時,v=v<SUB>0</SUB>,v<SUB>0</SUB>=H<SUB>0</SUB>r<SUB>0</SUB>,r=r<SUB>0</SUB>;,可得 K=H<SUB>0</SUB><SUP>2</SUP>-8πGρ<SUB>0</SUB>/3
因為宇宙再同一時刻各點由相同的H<SUB>0</SUB>;和ρ<SUB>0</SUB>;,且在任何時刻上述能量守恆式的成立,故對宇宙內任何一點,K為相同的常量,且此常量不會隨t而變化。
引入宇宙普適常量K後,藉助於前面給出的K-v關係式,可以將P相對O的速度表述為
此式對任選的O、P點均成立。v取正時表示v沿r的正方向,v取負時表示v沿r的負方向。下面分三種情況進行討論。
1.K>0
對應機械能E<SUB>0</SUB>>0。若初態v>0,則r將一直增至無窮大;若初態v<0,開始時r減小,宇宙收縮到一點後,r將沿反方向增大,直至無窮。這樣的宇宙,是一個無限膨脹的宇宙。
2.K<0
對應機械能E<SUB>0</SUB><0。為使v表述式中的根號內不出現負值,要求r≤r<SUB>max</SUB>=-8πGρ<SUB>0</SUB>r<SUB>0</SUB>/3K
當r=r<SUB>max</SUB>;時,v=0,即r將在r<SUB>max</SUB>;和-r<SUB>max</SUB>;之間往返振盪。這樣的宇宙是一個振盪的宇宙。
3.K=0
對應機械能E<SUB>0</SUB>=0。此時可解得H<SUB>0</SUB><SUP>2</SUP>=8πGρ0/3
在牛頓宇宙學中,這一解與K>0(即E<SUB>0</SUB>>0)的解本質上一致。或者一開始就是膨脹(對應v>0),便膨脹到無窮遠;或者一開始為收縮(對應v<0),收縮到一點後反向膨脹到無窮遠。兩者的區別僅在於K>0(即E<SUB>0</SUB>>0)時,膨脹到無窮遠,速度也不會減小到零,而當K=0(即E<SUB>0</SUB>=0)時,膨脹到無窮遠,速度會減小到零。
取正向膨脹,即取
且將r=0的時刻作為計時起點t=0,則由上式可解得r隨t的變化關係為
r=r<SUB>0</SUB>;的時刻t<SUB>0</SUB>;與H<SUB>0</SUB>;的關係為 t<SUB>0</SUB>=2/3H<SUB>0</SUB>
t<SUB>0</SUB>;時刻是隨意取的H0=α(t<SUB>0</SUB>;)是與t<SUB>0</SUB>;相應的量,因此任意時刻t均對應有 t=2/3H,H=α(t)
宇宙年齡
現代宇宙大爆炸理論認為,宇宙初態是全部物質濃縮在相當小的區域(可簡單說成是一個奇點)中,該時刻為宇宙起源時刻,即為絕對的t=0時刻,與牛頓宇宙學不同的是這裡不存在比t=0更早的時刻。而後宇宙急劇膨脹,即所謂爆炸,t時刻與觀察者相距r處宇宙物質,相對觀察者徑向遠離的速度為v=Hr,這一現象首先由哈勃通過天文觀察得出,故稱H為哈勃常數。
從宇宙誕生到t<SUB>0</SUB>;時刻,物質最遠只能運動到 R<SUB>0</SUB>=ct<SUB>0</SUB>=2c/3H<SUB>0</SUB>;的距離,這是因為狹義相對論知識告訴我們,任何物質的運動速度均不可能超過真空光速。在宇宙學中,稱R<SUB>0</SUB>;為t<SUB>0</SUB>;時刻的哈勃半徑,這也是天文上能觀察到的最大半徑。估算可知宇宙年齡大約80億年。
</BLOCKQUOTE>
物體的動能
v=Hr 可推導出 a=HHr 即加速度與距離成正比,係數是哈勃常數的平方。膨脹力f=mHHr 此力在r上所做的功W=1/2 mHHrr 即1/2 mvv 可用積分很容易導出這個結果。物體的動能等於膨脹力對物體所做的功。物體想要回到球心並靜止所需要的功是此動能的兩倍。當v=C 時就得出質能關係公式 E=mCC
光速問題
存在一個只以光速膨脹的宇宙,即C=Hr 那么這個宇宙中有大部分的是不可以光來測量觀測的,因為這個球體最大的弧線距離S等於圓周率與半徑的乘積,雖然光速隨宇宙歷史越來越快,但總有它達不到的地方,這些看到的地方從宇宙球的切面看,要占兩倍圓周率的倒數大小,只是宇宙切面總面積的一小部分。
膨脹係數並非各處相等的問題
由於質量的存在,物體必然要改變它沒有質量或者質量較小時的運動,這種改變體現為引力的存在,存在一種狀態,引力等於膨脹力,這時如果各處膨脹係數相等的話,那么任何兩個物體的引力質量就必然相等,這隻有在電荷的世界裡存在的情形無法解釋大尺度宇宙中星球質量不同的觀測。
宇宙的密度