牛頓問題

牛頓問題，因由牛頓提出而得名，也有人稱這一類問題叫做牛吃草問題。英國著名的物理學家牛頓曾編過這樣一道題目：牧場上有一片青草，每天都生長得一樣快。這片青草供給10頭牛吃，可以吃22天，或者供給16頭牛吃，可以吃10天，期間一直有草生長。如果供給25頭牛吃，可以吃多少天？這種類型的題目就叫做牛頓（牛吃草）問題，亦叫做消長問題。

基本介紹

• 中文名：牛頓問題
• 外文名：Newton Problem
• 別稱：牛吃草問題
• 表達式：牛吃的草量-—生長的草量= 消耗原有的草量
• 提出者：牛頓
• 提出時間：17世紀上半紀
• 套用學科：數學
• 適用領域範圍：奧林匹克數學、公務員考試數量關係
• 別稱：消長問題

簡介

牛頓問題又稱牛吃草問題或消長問題，是17世紀英國偉大的科學家牛頓提出來的。

典型牛吃草問題的條件是假設草的生長速度固定不變，不同頭數的牛吃光同一片草地所需的天數各不相同，求若干頭牛吃這片草地可以吃多少天。由於吃的天數不同，草又是天天在生長的，所以草的存量隨著吃的天數不斷地變化。

基本公式

解決牛吃草問題常用到四個基本公式，分別是︰
（1）草的生長速度= （對應的牛頭數×吃的較多天數－相應的牛頭數×吃的較少天數）÷（吃的較多天數－吃的較少天數）；
（2）原有草量=牛頭數×吃的天數－草的生長速度×吃的天數；`
（3）吃的天數=原有草量÷（牛頭數－草的生長速度）；
（4）牛頭數=原有草量÷吃的天數+草的生長速度。
這四個公式是解決牛頓問題的基礎。
由於牛在吃草的過程中，草是不斷生長的，所以解決消長問題的重點是要想辦法從變化中找到不變數。牧場上原有的草是不變的，新長的草雖然在變化，但由於是勻速生長，所以每天新長出的草量應該是不變的。正是由於這個不變數，才能夠導出上面的四個基本公式。

解題關鍵

牛頓問題，稱“牛吃草問題”，牛每天吃草，草每天在不斷均勻生長。解題環節主要有四步：

1、求出每天長草量；

2、求出牧場原有草量；

3、求出每天實際消耗原有草量( 牛吃的草量-生長的草量= 消耗原有的草量)；

4、最後求出牛可吃的天數。

想：這片草地天天以勻速生長是分析問題的難點。把10頭牛22天吃的總量與16頭牛10天吃的總量相比較，得到的10×22-16×10=60，是60頭牛（22-10）天吃的草，平均分到（22-10）天裡，便知是5頭牛一天吃的草，也就是每天新長出的草。求出了這個條件，把所有頭牛分成兩部分來研究，用其中一部分吃掉新長出的草，用另外一部分吃掉原有的草，即可求出全部頭牛吃的天數。

設一頭牛1天吃的草為一份。

那么10頭牛22天吃草為1×10×22=220(份)，16頭牛10天吃草為1×16×10=160(份)

（220-160）÷（22-10）=5(份)，說明牧場上一天長出新草5份。

220-5×22=110（份)，說明原有老草110份。

綜合式：110÷（25-5）=5.5(天)，就能算出一共多少天。

如果想求出有多少牛，那么題目一定會告訴原來的草量，方法就和求草一樣。可以先寫出求草的算式，再帶入數字。

題目解法

在牧草不生產的條件下，如果12頭公牛在四星期內吃掉三又三分之一由格爾（當時牛頓想出問題並解出答案的地方）的牧草，則按比例36頭公牛四星期內，或16頭公牛九個星期內，或八頭公牛18星期內吃掉10由格爾的牧草，由於牧草在生長，所以21頭公牛9星期只吃掉10由格爾牧草，即在隨後的五周內，在10由格爾的草地上新長的牧草足夠21-16=5頭公牛吃9星期，或足夠5/2頭公牛吃18個星期，由此推得，14個星期（即18個星期減去初的四個星期）內新長的牧草可供7頭公牛吃18個星期，因為5：14=5/2：7。前已算出，如牧草不長，則10由格爾草地牧草可供8頭公牛吃18個星期，現考慮牧草生長，故應加上7頭，即10由格爾草地的牧草實際可供15頭公牛吃18個星期，由此按比例可算出。24由格爾草地的牧草實際可供36頭公牛吃18星期。

牛頓還給出代數解法：他設格爾草地一個星期內新長出的牧草相當於面積為y由格爾的草地，又每頭公牛每個星期所吃牧草所占的面積是相等的。根據題意，設若所求的公牛頭數為x，就為（10/3+10/3*4y）/(12*4)=(10+10*9y)/(21*9)=(24+24*18y)/18x，解得x=36，即36條公牛在18個星期內吃掉24由格爾的牧草。

還有一種方法就是使用方程式的解法。

例如有一塊牧場，可供9頭牛吃3天，或者5頭牛吃6天，請問多少牛能夠2天吃完？

做方程式：設牧場原有草量為y，每天新增加的牧草可供x頭牛食用，N頭牛能夠2天將草吃完，根據題目條件，列出方程式：

解方程組得

其實這種牛吃草問題的核心公式是：原有草量=（牛數-單位時間長草量可供應的牛的數量）×天數。

另一解法：

牛吃草問題的關鍵點在於這個問題隱藏了一個基本的平衡在其中，那就是：假若每頭牛每天的吃草速率和吃草量都不相同，那么此題無解。因為很可能一頭牛心情好一天就能吃完這些草，也可能10頭牛食慾不佳一個月吃都不完這些草，因此每頭牛每天的吃草速率和數量必須都是相同的是這個問題成立並且能夠得到答案的充要條件。

得到這個結論後，就要開始確定一個平衡的方程式出來。不難想到，可以是吃草量和草本身量之間的平衡，也就是吃草量=草總量。於是可以假設一頭牛一天的吃草量為1個單位，並假設第三種情況牛吃草的天數為N；接下來開始尋找平衡方程，可以看到在問題提供的條件中，第一種情況的草的總量為10×22，第二種情況的草的總量為16×10，第三種情況的草的總量為25×N。

然後尋找方程的平衡：既然現在已經找到三種情況里草地的總量，那么不難想到方程的另一邊就要靠草的量來進行平衡，於是，假設原有草量為Y，草每天的生長量為X，得到如下方程組：

解此方程組，可得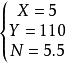

因此25頭牛用五天半的時間就能吃完這些草。

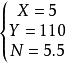
規律總結

牛頓問題的難點在於草每天都在不斷生長，草的數量都在不斷變化。解答這類題目的關鍵是想辦法從變化中找出不變數，可以把總草量看成兩部分的和，即原有的草量加新長的草量。顯而易見，原有的草量是一定的，新長的草量雖然在變，但如果是勻速生長，也能找到另一個不變數——每天（每周）新長出的草的數量。

基本思路：假設每頭牛吃草的速度為“1”份，根據兩次不同的吃法，求出其中的總草量的差；再找出造成這種差異的原因，即可確定草的生長速度和總草量。
基本特點：原草量和新草生長速度是不變的；
關鍵問題：確定兩個不變的量。
基本公式：
生長量=（較長時間×長時間牛頭數-較短時間×短時間牛頭數）÷（長時間-短時間）；
原有草量=較長時間×長時間牛頭數-較長時間×生長量；