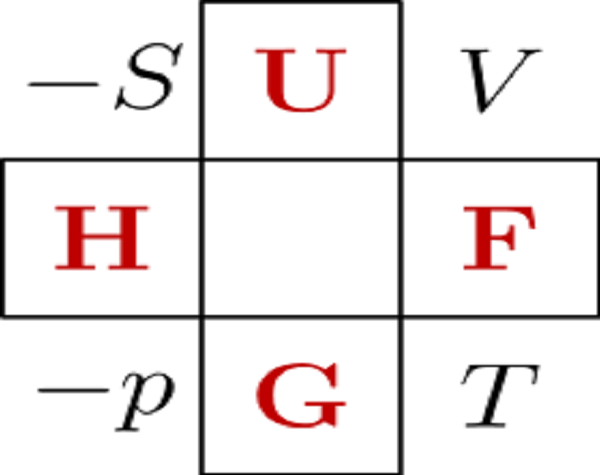熱力學方格

熱力學方格（英語：thermodynamic square），又稱為熱力輪（thermodynamic wheel）、古根海姆圖（Guggenheim scheme）或玻恩方格（Born square），是由馬克斯·玻恩提出的一種記憶術，用於快速建構熱力學關係式。1929年，玻恩在課堂中提出熱力學方格。F·O·柯尼希（Koenig）的論文中曾提及熱力學的對稱性。方格角落為共軛變數，而四邊則是熱動力位能。變數之間的放置和關係是記憶它們構成關係的關鍵。

基本介紹

• 中文名：熱力學方格
• 外文名：thermodynamic square
• 學科：物理

使用

熱力學方格主要用於計算任何感興趣的熱力學勢的導數。假設例如一個期望計算衍生物的的內部能量 。應考慮以下程式：

1）將自己置於感興趣的熱力學潛力中，即（ ）。在我們的例子中，那就是 。

2）感興趣的勢頭的兩個相對角表示整體結果的係數。如果係數位於正方形的左側，則應添加負號。在我們的例子中，中間結果將是 .

3）在每個係數的對角，您將找到相關的差分。在我們的例子中，對面的角落 將會 （卷）和對面的角落 將會 （熵）。在我們的示例中，中期結果將是： 。請注意，符號約定僅影響係數而不影響差異。

4）最後，總是添加 ，在哪裡 表示化學勢。因此，我們會有： 。

熱力學平方也可用於找到麥克斯韋關係。望著廣場的四個角落，製作一個 形狀，人們可以找到

通過旋轉 形狀（隨機，例如逆時針旋轉90度成一個 形狀）其他關係如：

可以被找尋到。

最後，每一側中心的電位是該側角落處變數的自然函式。因此，G是p和T的自然函式，U是S和V的自然函式。

與麥克斯韋的關係

1）要選擇的是兩個狀態變數，它們位於正方形公共邊的兩個角上。

例如：找一個麥克斯韋關係與 和 它形成了左邊緣的角落。這些形成了所尋求的麥克斯韋關係的左側的微分商，即

2）限制正方形相對側的狀態變數形成所尋求的麥克斯韋方程右側的微分商。確保以與第一條邊相同的方向讀取它們。

相反的 和 位於 和 ，我們有 形成，所以“上角派生到下角”。因此，必須導出廣場“從上到下”的另一側。中期結果如下：

3）差異商，兩者兼而有之 同樣 包含一個負號，因為兩個（！）符號都在帶有減號的邊上。

左側收到負號。中間結果如下：

4）頁面的常量保持變數總是在另一側的分母中找到。

最終結果如下：