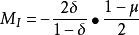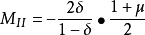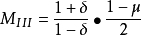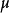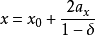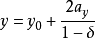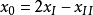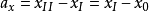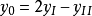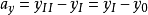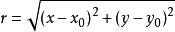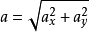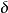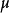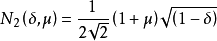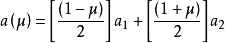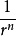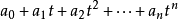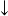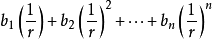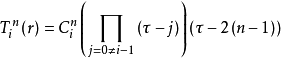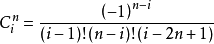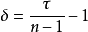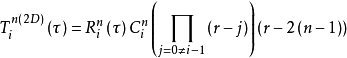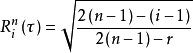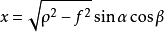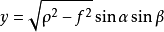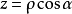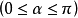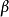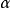無限元的提出
在水利、地震、岩土、海洋和爆破等實際工程中, 常常會涉及到無界域問題。這類問題中為數不多的幾個情形,如均質無限彈性空間在集中力或分布力作用下的應力分析,均質無界域中的圓孔內承受
均布荷載作用等,通過數學手段,可得到
解析解。對於比較複雜的工程實際問題,要獲得解析解就非常困難,只能藉助於數值途徑。有限元法的出現和迅速發展,為解決這一問題提供了強有力的數值手段。然而,在有限元單元尺寸和數目之“有限”與無界域之“無限”間必須進行折中和妥協,其中最自然的做法就是保留有限元法的所有特徵,而對無界域進行近似處理,即人為截取“足夠大”的區域進行幾何上的格線剖分,同時在“人為” 邊界上施加相應的近似約束邊界條件。這種方法雖然不需引入新概念,但在對“足夠大”的界定上讓人感到很無奈:區域較小對數值計算規模的控制很有利,但在理論上會帶來較大誤差;區域較大能減小理論誤差,但數值計算規模將以級數倍增加。另一方面,對 于波動問題,“人為”邊界上的約束條件對求解精度影響很大,因為任何“人為”邊界的存在,都會產生“本來就不存在的”波的反射,從而影響感興趣區域(近場)上的求解精度。
實際上,處理無界域問題還可以採用這樣一種方式,引入一種幾何上無限大的“有限”單元,再對其在物理上進行界定,這就是無限元法思想的由來。無限元這一術語1977年由Bettess 和Zienkiewicz第1次使用,在概念上它是有限元的延伸,是一種幾何上可以趨於無限遠處的單元,即它所占的區域是無限的;又由於無限元必須反映近場的邊界特徵或與模擬近場的有限元結合,它實際上只在一個方向趨於無限,因而又被稱為半無限元。由於有限元的概念涵蓋所有占非無窮小區域的單元,廣義地講,無限元仍然屬於有限元的範疇。總之,無限元為克服有限元在解決無界域問題時而提出,常常與常規有限元同時用來解決更複雜的無界問題,是對有限 元方法的一種補充,因而它與有限元方法的“協調” 與生俱在,比邊界元等其它求解無界域問題的數值方法更具有優勢。
無限元的要素
下圖所示為一典型的二維“四邊形”無限單元。 I、II、III,IV這4個結點是構成該無限元幾何形狀的最基本要素:I、II間的連線是無限單元的邊界,當然,可以增加結點以描述曲線邊界;I~III和II~IV是無限單元的邊,分別趨於無限遠處;I、II兩點稱為無限單元的角結點,III、IV稱為無限單元對應邊的中結點。無限單元在幾何上比較簡單,它的兩條邊在笛卡兒坐標系中始終保持為直線,這就是說,用I~III和II~IV兩條直邊已足夠描述無限單元的幾何特徵。無限單元通過它的邊與相鄰的無限單元或趨於無限的邊界相連,通過它的邊界反映近場信息,或與近場的有限單元相連。
無限單元與有限單元的一個重大區別是前者具有方向性,即I、II、III、IV這4個結點在局部坐標系中的順序是固定的。無限單元在幾何上的一個重要特點是兩條邊在趨於無窮的方向上不能相交, 在數學上就是要求無限單元在無限方向上必須是發散的,只有這樣,才能保證物理量在趨於無限過程中的一致單調性。對所生成的無限單元,必須逐個檢查以保證符合該條件。
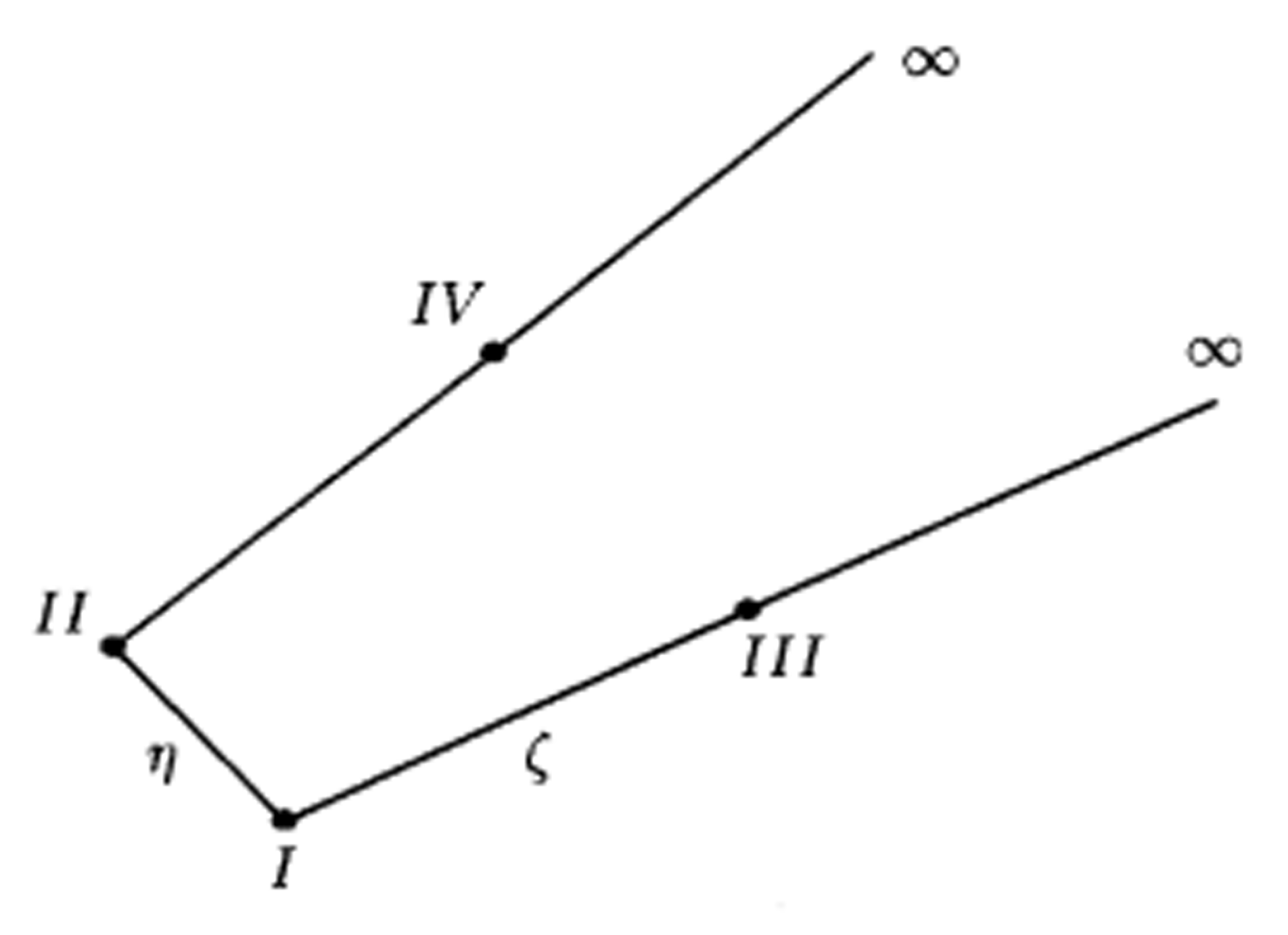 二維無線單元及其要素
二維無線單元及其要素常規無限元方法
1.Astley映射共軛無限元
對於上圖所示的二維無限單元,其整體坐標與局部坐標間的幾何映射為:
其中,幾何映射函式為:
顯然,沿無限元的兩條邊,例如I~III(
=-1)邊,映射即變成為:
Astley將點(
,
)稱為虛擬聲源,r為相對於虛擬聲源的距離,a表示無限單元邊界相對於虛擬聲源的距離,即a=r(
=-1)。以二維為例,聲輻射問題的聲壓 p(x,y)由Helmholtz方程:
其中
為二維Laplace運算元,k=w/c為所考慮問題的波數。
據此,可構造出沿
方向無限單元形狀函式的幅值部分。對於1階單元(沿
方向假定是線性的), 形式為 :
另外,還通過下列表示無限單元邊界位置的量:
構造了不隨結點變化的形狀函式的相位部分,其形式為:
首次將無限幾何映射和形狀函式的研究分開處理,形狀函式的構造分為幅值衰減部分和相位部分。無限單元的變階特性體現於幅值衰減部分。
使用n個自由度,聲壓在母單元內的n階多項式逼近在實際單元中可產生最高到
次冪的展開,如下列對應關係:
在有限的幾何映射點之間(即圖1的I~II或 III~IV之間)等距離地取n個聲場插值結點,構造出徑向形狀函式為:
=0~(n一1)分別對應於
處的n個結點,第n+1個結點設定在無限遠處,顯然,上式只適應於主導衰減特性為1/r型 的三維或軸對稱聲傳播問題,對於主導衰減特性為 1/
型的二維問題,為了獲得這種主導形式,必須 給式的形狀函式乘以
因子,變成為:
2.Burnett無限元
1994年, Burnett採用共焦橢圓變換,即:
研究扁長形橢球結構(如潛艇)的聲輻射問題。上式中,
代表考察點所處橢球的半長軸;
為極角,即雙曲面漸近錐張開角的一半;
為關於Z軸的圓周角;f為共焦橢圓公共的半焦距,為常數。這樣,複雜的三維無界域就分解成無限的
方向與兩個有限的
,
方向。
Burnett元的優點是顯然的,也是很突出的,它在求解大縱橫比結構的聲輻射/散射問題時,可以大大降低用於模擬複雜近場的有限單元數目,從而數百倍地提高這類問題的數值分析效率.該工作已被視作無限元領域的“突破性發現”。
無限單元法的套用
無限單元是為了克服有限單元在求解無界域問 題時的不足而提出的,因而,原則上說,可以用有限元方法求解,但涉及無界域的物理問題,都特別適合於用無限元方法求解.無限元方法自從提出以來,在自身不斷發展的過程中,已有效地解決了許多實際工程問題.
從無限元方法的發展來看,理論研究主要針對淺水表面波、聲輻射/散射等標量場問題.對於如彈性波等向量場問題,是無限元方法應該涉及的一個重要 方面,其研究內容包括:根據地層運動反演和預測地震;根據地層的特殊結構探測煤炭和石油;等等.雖然已經開始此類工作,但理論上還很初步,與聲輻射等問題的成果相比,還需要開展更深入的研究.另一方面,由於單元格線的局限,常規有限元法在求解短波問題時遇到了嚴峻的挑戰,對於相伴的無限元法也隨之提出了新課題。
其它無限元方法簡介
有限元法將連續的有界域轉變為離散型的結構,從而實現無限維連續空間的有限維離散逼近;再利用基函式(如項式)對所求的場函式進行插值;然後採用相應方法(如變分法),建立以結點值為待定參數的線性方程組,最終獲得求解.因而,在理論上,有限子空間剖分越細,計算將越精確.考慮到結構剖分的限度對複雜問題精度的限制,應隆安將無限剖分思想與有限元方法結合,提出了“允許使用無 窮多個單元剖分”的“無限元方法”,即基於有限元方法,使用無窮多個而不是有限個單元.近年來,應隆安等分別研究了三維守恆律有限元方法逼近光滑解的誤差估計、提出了多維守恆律方程組的二階顯式有限元格式,並證明了其收斂性、研究了雙曲型守恆律方程組的Godunov格式中離散激波的漸近穩定性,還將這種無限元方法用於模擬無界的多連通區域、修復體唇側頸緣出現的應力集中等問題。
 二維無線單元及其要素
二維無線單元及其要素