無粘性流,是非定常不可壓粘性/無粘性耦合方程的一種分步分解方法。
基本介紹
- 中文名:無粘性流
- 定義:是一種分步分解方法。
- 作者:王連澤
- 所屬類別:數學
摘要
引言
內渦旋中υt/r=const
外渦旋中υt·rn=const
實際上,流體粘性的影響絕非是不取n=1所能體現的。筆者經實驗發現,n是徑向距離r的函式。因此為更準確地描述切向速度的分布規律,必須充分考慮流體粘性的影響,尋求更準確的數學表達形式。
安裝減阻桿後,對旋風除塵器內的流動已不能再作二維軸對稱流動的假定。筆者基於繞流理論,推導了安裝不同類型減阻桿後的切向速度的計算公式,根據這些公式計算的結果均能與實驗結果較好地吻合。限於篇幅,本文僅給出安裝圓形斷面減阻桿時切向速度公式的推導過程。本文的實驗數據是在340mm筒徑的Stairmand高效旋風除塵器模型上取得的。實驗中,控制旋風除塵器的入口速度為19.5m/s。
2無粘性假設時計算結果與實驗結果的比較
在整個外渦旋中,擬合切向速度對徑向距離的分布,得到平均的分布指數n=0.73。將n取作定值計算結果與實驗結果的比較如圖1所示。
無粘性流
 無粘性流
無粘性流從圖中可看出將n取為固定值0.73時,切向速度計算結果與實驗結果的差別。特別是在內外渦旋交界面及其附近區域,該差別是非常大的。考慮到內外渦旋交界面及邊壁附近的n值與在整個外渦旋中的均值差別較大,故擬合中捨棄兩端點,由此所得的平均n值為0.75,將此n值切向速度計算結果一併繪入圖1中。由此可見,雖然此時在內外渦旋交界面及其附近區域誤差變小,但在外渦旋的大部分區域誤差卻增大。因此,n值無論如何選取,無論作何種修正,只要將其取為定值,便會產生很大誤差。
3粘性流體切向速度計算公式的推導及其計算結果與實驗結果的比較
設粘性流場中包圍一固定體積V的封閉表面積為S,用符號Ω代表旋度,則在dt時間內從S表面輸出旋度
無粘性流
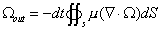 無粘性流
無粘性流式中μ--流體動力粘度,Pa·s。
對上述套用高斯積分定理,及考慮在dt時間內,V內旋度減少
無粘性流 (2)
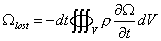 無粘性流
無粘性流可得平衡關係
無粘性流 (3)
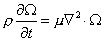 無粘性流
無粘性流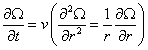 無粘性流
無粘性流由初始條件、終止條件及邊界條件可得式(4)的特解
無粘性流 (5)
無粘性流
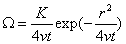 無粘性流
無粘性流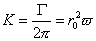 無粘性流
無粘性流式中:
無粘性流--環量,m2/s;
r0--內外渦旋交界面半徑,m;
ω--旋轉角速度,s-1。
又根據環量等於旋度乘以環流面積,r圓面積的環量為
無粘性流
 無粘性流
無粘性流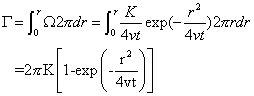 無粘性流
無粘性流無粘性流(8)
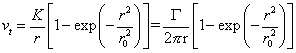 無粘性流
無粘性流無粘性流
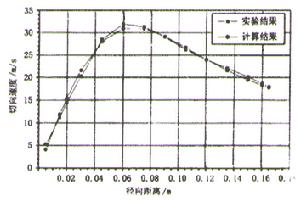 無粘性流
無粘性流由圖2可以看出,基於粘性流體考慮推導所得切向速度分布計算公式的計算結果與實驗結果吻合很好。
4加裝圓形斷面減阻桿後切向速度計算公式的推導及其計算結果與實驗結果的比較
根據流體繞流圓柱體的流動規律可推導出安裝圓形斷面減阻桿時切向速度的計算公式。參見圖3(C為源點,B為匯點)。
無粘性流
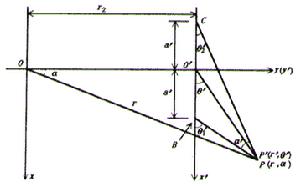 無粘性流
無粘性流假定等強源流和匯流的流函式
無粘性流
 無粘性流
無粘性流式中:Q--源流(匯流)強度,m2/s。
套用正弦定理及令M=2a'Q為偶極矩,則有:
無粘性流
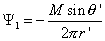 無粘性流
無粘性流來流的流函式
無粘性流
 無粘性流
無粘性流對上式積分並按泰勒級數展開,然後再進行坐標變換,得
無粘性流
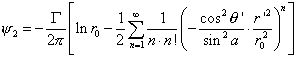 無粘性流
無粘性流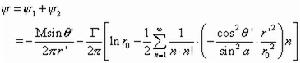 無粘性流
無粘性流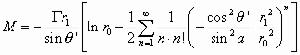 無粘性流
無粘性流將(14)代入(13)再進行坐標變換,得
無粘性流
 無粘性流
無粘性流其中無粘性流
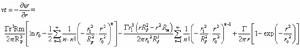 無粘性流
無粘性流 無粘性流
無粘性流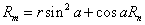 無粘性流
無粘性流 無粘性流
無粘性流式(16)表明切向速度與流體在旋風除塵器內的旋轉角度有關,即減阻桿的引入改變了原來軸對稱的流動規律。
由取a為不同數值時的計算結果與實驗結果的比較可知,當a接近30°時,流動已趨於穩定且與實驗數據能較好吻合,故本文將a取為30°。利用公式(16)計算所得的切向速度值與實驗結果的比較如圖4所示。
無粘性流
 無粘性流
無粘性流圖4表明,按來流流函式與假想偶極子流函式疊加計算所得的切向速度值與實驗數據的吻合程度是比較好的。誤差產生的原因是由於公式推導過程中沒有考慮流體的螺旋運動。實驗流體繞流後,經過一周旋轉,下降了一定高度又要重新繞流,也就是在分離器高度上與偶極流疊加的來流速度是不斷變化的。但是,實驗結果表明,加裝減阻桿後與常規旋風除塵器一樣,切向速度沿軸向的梯度很小,似乎在旋風除塵器高度上,來流速度是不變的。因此,上述的推導方法又是可取的。因按理論推導所得公式計算的結果與實驗結果能達到較好吻合,故本文中未對流體的螺旋運動進行修正。
5結論
因充滿分考慮了流體的粘性,故本文推導所得的切向速度計算公式能與實驗結果很好吻合,這為旋風除塵器分離效率和流動阻力等的準確計算提供了可能。從偶極子繞流出發,本文推導的安裝減阻桿後的切向速度計算公式亦能與實驗結果較好地吻合。基於粘性流體理論,如何推導旋風除塵器內軸向速度和徑向速度的數學表達式,將是筆者進一步研究的目標。
參考文獻
2.MKessler.Flowmeasurementandefficiencymodelingofcyclonesforparticlecollection.AerosolScienceandTechnology.1991,15:8-18.
3.寧晃,等.燃燒室氣動力學.北京:科學出版社,1987.
4.童秉綱,等.非定常流與渦運動.北京:國防工業出版社,1993.
5.張仲寅,等.粘性流體力學.北京:國防工業出版社,1989.
6.周謨仁.流體力學泵與風機.北京:中國建築工業出版社,1985.
