無窮項加權算法，是建立在有窮項加權算法上的，因“無窮項加權”難以進行直觀計算而產生的算法。
前提是權重的總和為1，且每一項擁有一個“原始值”，即未經加權的值。有窮項加權中，每一項的權重是一個常數，如：10%、40%、0.03，因而權重的總和才能為1。而無窮項加權中，可能會存在一種很不理想的情況，那就是每一項（或者部分項，在此不討論）的權重為0，這樣看來，所有權重的總和的確“可能為1”（因為有無窮項）。這就讓計算這些無窮項加權成為一道難題，因為在普遍加權算法中，我們通過“每一項的原始值”乘以“每一項的權重”，全部累加以得到最終加權平均值；而在這些無窮項加權中，因為“每一項的權重”是0，那么“每一項的原始值”乘以“每一項的權重”還是0，如此一來，最終的加權平均值完全無法計算。本詞條將介紹並證明無窮項加權算法，以解決諸如此類的問題。
基本介紹
- 中文名：無窮項加權算法
- 外文名：Infinite term weighting algorithm
- 別名：無窮項加權平均值算法
- 適用領域：加權均值、數學期望、空間積分、數學建模等
- 套用學科：數學、物理等
普遍加權算法,有窮項加權,無窮項加權,思路及推導過程,套用領域,
普遍加權算法
每一項的原始值：每一項未經加權的值。如果沒有原始值，則加權無意義。因為加權是對於“值”而言的，不是對於“項”；比如，你可以對“語文成績的值”進行加權，但不能對“語文成績”這個名詞來加權。
有窮項加權
有窮項加權算法中，要加權的項數是有限的，即，項數是一個正整數。
例如，一個人的語數外3門成績分別按照30%、40%、30%的權重進行加權，得到的“最終成績”將會=語文成績*30%+數學成績*40%+英語成績*30%。在這裡，權重的總和為1，項數為3（是一個正整數）；且每一項擁有一個原本值（即：未經加權的值），分別就是各科的成績。
稍微複雜一些的有窮項加權，假設有n項，並假設其中的第k項對應的值為F（k），對應的權重為W（k），則可算得最終加權平均值=
。
無窮項加權
無窮項加權算法中，要加權的項數是無限的，但這不一定意味著每一項的權重都為0。
例如，可以有一串待加權的無窮項的權重分別為：1/2、1/4、1/8、1/16……這樣的無窮項權重總和也為1，且每一項的權重都不為0，只是無窮趨近於0。然而，這樣的“無窮項加權”，可以直接使用有窮項加權中的公式：最終加權平均值=
，來算得最終加權平均值。因此這不是本詞條著重討論的內容。
還有一些情況，如某幾項的權重是一個常數，其餘項權重都是0。例如，有某一項的權重是40%，其餘項權重都是0，也就是說，其餘項權重總和為60%。這也的確是一種無窮項加權，但是那些權重為常數的項都可以用有窮項加權公式：加權平均值= ，來算得，然後撇開權重為常數的項，對權重為0的項進行計算。因此這也不是本詞條著重討論的內容。
本詞條著重討論：每一項的權重都為0的無窮項加權算法。
思路及推導過程
在這種情況下，每一項的權重都為0。但我們知道，這不是普通的0，最好的證明就是權重內部有高低之分，有比例之別。所以在這些眾多的0中，它們“內部”的大小還不一樣。這就使得思維更加抽象，容易走入死胡。
不妨逆轉一下思維。我們在此已經使用了一條鐵律：“權重的總和為1”，才會從“每一項的權重都為0”的思路開始。每一項權重都為0的確是一個事實，但是可以先把權重具象化，將權重內部的比例畫成函式表示出來。解釋一下這個函式，它的x軸其實可以看作是無窮個“項”的集合，y軸可以看作是權重*無窮。需要明確的是，x的值無意義，且x軸上的“一段長度”也沒有具體的意義，因此“dx”無意義。如果憑藉想像力去寫積分式子的話，總免不了乘上dx，因此可能寫出來的只是無意義的式子。如果不理解，還可以再用有窮項來解釋一下，如果將每一項與對應權重畫成一個函式，那么y軸就是每一項的權重，x軸上有零碎的幾個點，那就是各個項了。比如，“語文”可以是x軸上的一個點，不管它放在什麼x等於幾的位置，它都是一個叫“語文”的點。因此，x的值無意義，且x軸上的“一段長度”也無意義。
為了方便理解，我們從一道例題說起吧。有一位籃球運動員在練習投籃球，他的球會先打到籃板後反彈（可能進球）。假設籃球與籃板的接觸僅在一個點。俯視籃板，若籃板寬度忽略不計，籃板的俯視圖就是一條線段。假設這條線段長80cm，將它放在x軸上從-40到40（單位：cm）的位置，使之與x軸重合。在這裡，假定：“每一項”就是“籃球砸到籃板x=x0的位置”，“每一項的原始值”就是“籃球砸到籃板x=x0的位置後反彈能進球的機率F(x0)”。如果說有“權重函式W(x0)”，那么令它的含義是：“W(x0)代表籃球砸到籃板x=x0的位置的機率”。如果將每一個F(x0)與W(x0)相乘，並把這些乘積全部累加，就會得到最終加權平均值，其含義也就是這個籃球運動員任投一個打板球的進球機率。
只可惜，W(x0)=0。因為籃球能正好砸到籃板x=x0位置，這么精確的點，只有0的機率會出現。所以F(x0)與W(x0)相乘還是0。但是我們隱約會感覺到，砸到籃板各處的機率可能是會有所不同，會有高低大小之分。例如，這位籃球運動員可能比較容易將球投到偏中間一些的位置，不妨就設籃球砸到籃板偏中間位置的機率高吧。
這時我們拋開“權重總和=1”，先直接探究權重的內部比例，畫出其函式圖。x軸（定義域從-40到40）就是籃板俯視圖（籃板寬度不計），y軸是權重*無窮（這難以描述），但是整個圖像表現出來的是權重的內部比例，並存在特定的“比例形狀”，如函式y=sinx就是一種“比例形狀”，函式y=2x+1/x也是一種“比例形狀”；僅改變係數，比例形狀不變，如：y=sinx與y=3sinx的比例形狀相同；y=2x+1/x與y=4x+2/x的比例形狀也相同。因此稱這個函式為：“微小權重比例形狀函式”S(x)。從意義上去理解，S(x)與W(x)是成正比的，所以可以理解為S(x)=K*W(x)，K是一個係數。不過因為W(x)=0，S(x)是一個實數，所以K應是一個無窮大的數。
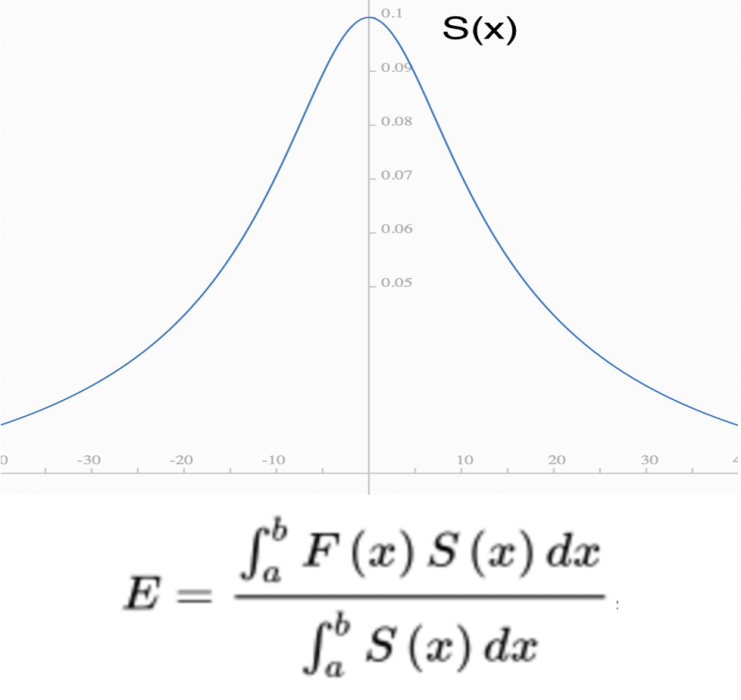
在本題中，因為籃球砸到籃板偏中間位置的機率較高，因此W(x)的值偏x=0處較高（儘管是0），因此S(x)的值偏x=0處較高。按照這樣的比例形狀，可以擬合出下面這樣的S(x)函式圖：
微小權重比例形狀函式S(x)
接下來，我們需要把K的值求出。此時要利用“權重總和=1”，即：
。因為S(x)=K*W(x)，等式左右兩邊同時求和，即
，因此
。
再按照普遍加權算法公式，可得：
最終加權平均值=
。
這樣之後，就可以用“離散”的方式把x軸分成正無窮份，用計算器試數得到答案，比如令份數=1000、10000、100000以無限逼近答案。但如果函式並不包含離散點，滿足一定的連續條件，那么還可以再進行一步。
注意到，分母與分子的維度都是“一段長度”（儘管是無窮長）；但如果函式F(x)*S(x)與S(x)都不包含離散點，滿足一定的函式連續條件，就可以分數上下同乘dx，注意到幾何意義，即可得到“一塊面積”的維度。於是：
結論：
（在函式F(x)*S(x)與S(x)都不包含離散點的情況下），其中，a、b代表積分上下限，S(x)代表“微小權重比例形狀函式”。
套用領域
無窮項加權算法在許多領域中都有套用，如：數學期望、空間積分、數學建模。以空間積分為例，在空間中，一個空間方向是比較難以“均勻”地表述的。在二維平面直角坐標系中，以點（0，0）為起點，方向的均勻變化可以用角度來表示，因為角度的變化與方向的變化速率是相同的，因而“均勻”。但是在三維空間中，沒有一個單一變數與“方向”的變化速率相同，方向往往需要兩個變數來表示，因而用任一變數來表示則“不均勻”（如果用兩個變數來表示，則至少有一個變數“不均勻”，需要調和）。有時如果想在空間中進行一些積分，可能會要求“方向變化均勻”，此時就需要調節變化和方向不均勻的變數，方式便是加權。舉個例子，想要在以1為半徑的球的球面上“均勻取無數個點”（即方向要均勻），每個點對應一個“原始值”（原始值可與該點x、y、z坐標有關），欲求所有“原始值”的平均值。因無法用與空間方向變化速率相同的變數來表示一個點的坐標，可以分兩步：向量1:（1，0，0）以點（0，0，0）為圓心，在x-y面內沿俯視逆時針轉過角度
，得到向量2；向量2再以點（0，0，0）為圓心，在自身與點（0，0，1）圍成的平面內向z0方向轉過角度
。如果按這樣的順序積分，若把這個球看成上下分別為北極南極點的地球，則維度高的地方顯然取到的點更加密集。此時就要進行加權，讓維度較高的點乘以較小的權重，維度較低的點乘以較大的權重，以達到“取點均勻”（改變數值占的權重的同等效果就是改變了取點密度）。事實上，經計算，此處的“微小權重比例形狀函式”：
。
