兩齒輪在嚙合傳動時，其節點P的圓周速度方向與嚙合線N1N2之間所夾的銳角，稱為漸近角（approach angle），通常用α'表示。
基本介紹
- 中文名：漸近角
- 外文名：approach angle
- 領域：機械齒輪
定義,分類,相關概念,
定義
兩齒輪在嚙合傳動時，其節點P的圓周速度方向與嚙合線N1N2之間所夾的銳角（圖1），稱為漸近角，通常用α'表示。
圖1 漸開線直齒圓柱齒輪的嚙合傳動
圖1 漸開線直齒圓柱齒輪的嚙合傳動而兩個齒輪之間的漸近角隨齒輪種類、性質的改變而改變。下面將介紹常見齒輪的漸近角性質。
分類
漸開線直齒圓柱齒輪的嚙合傳動
（1）當兩直齒輪按標準中心距安裝時
當兩齒輪嚙合的時候，節圓總是相切，而當兩齒輪按標準中心距安裝的時候，兩輪的分度圓也是相切的，此時兩齒輪的節圓與分度圓重合。
此時漸近角為α'（如圖1）。由此定義可知，漸近角等於節圓壓力角。且由於按照標準中心距安裝，漸近角也等於分度圓壓力角。
（2）當兩輪的實際中心距a'與標準中心距a不相同時，漸近角與分度圓壓力角不再相等。
此時齒輪中心距與漸近角的關係為：a'cosα'=acosα
如增大兩圓中心距（如圖2），此時兩圓的分度圓互相分離。兩圓的節圓半徑大於分度圓半徑，其漸近角也大於分度圓的壓力角a。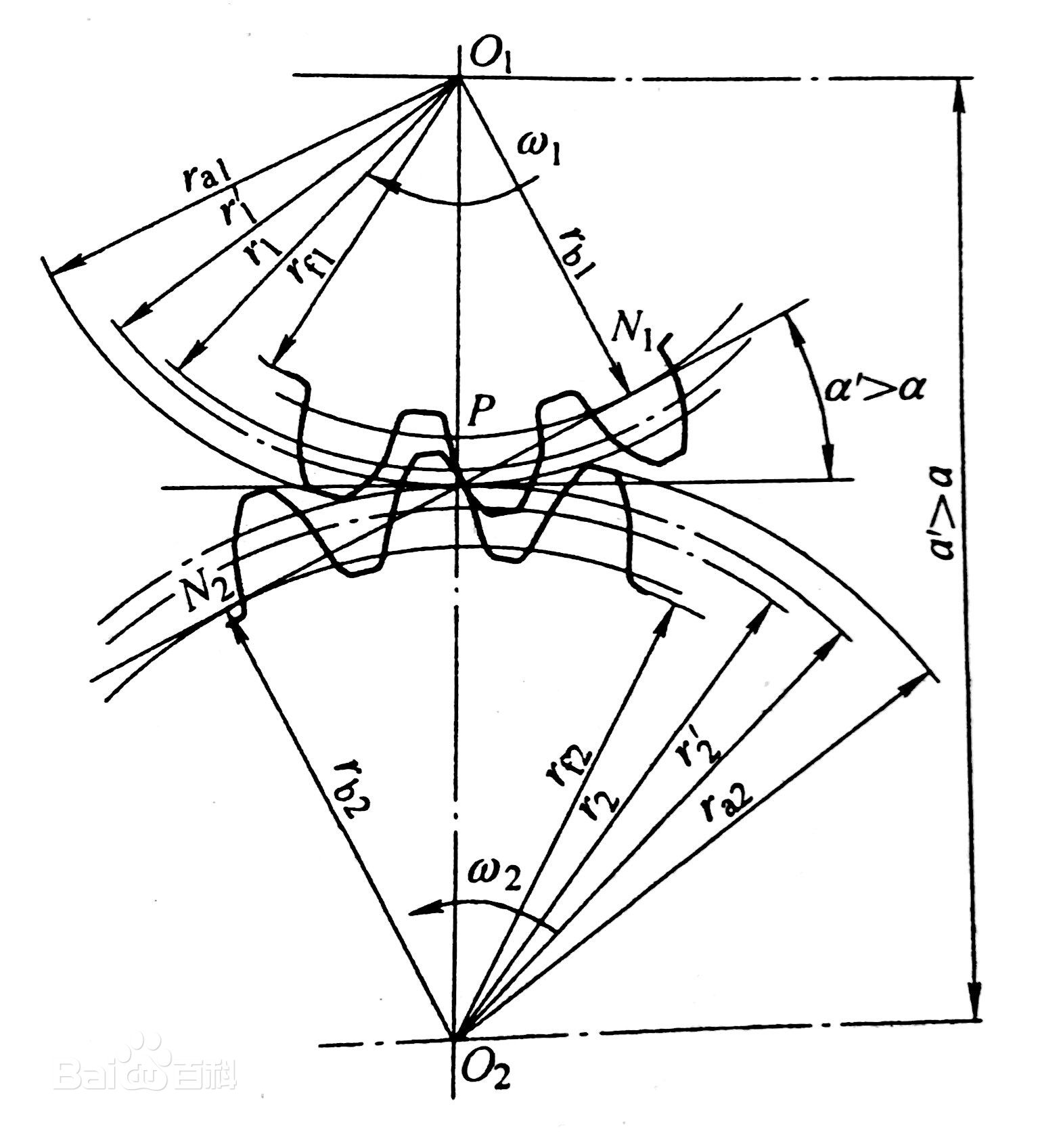
圖2 增大中心距後漸近角變化
圖2 增大中心距後漸近角變化齒輪與齒條傳動
如圖3，齒輪與齒條傳動，無論是否為標準安裝，嚙合線N1N2及節點P的位置始終保持不變。故齒輪的節圓恆與其分度圓重合，其漸近角α'恆等於其分度圓壓力角a。只是非標準安裝時，齒輪的節線與其分度線不再重合。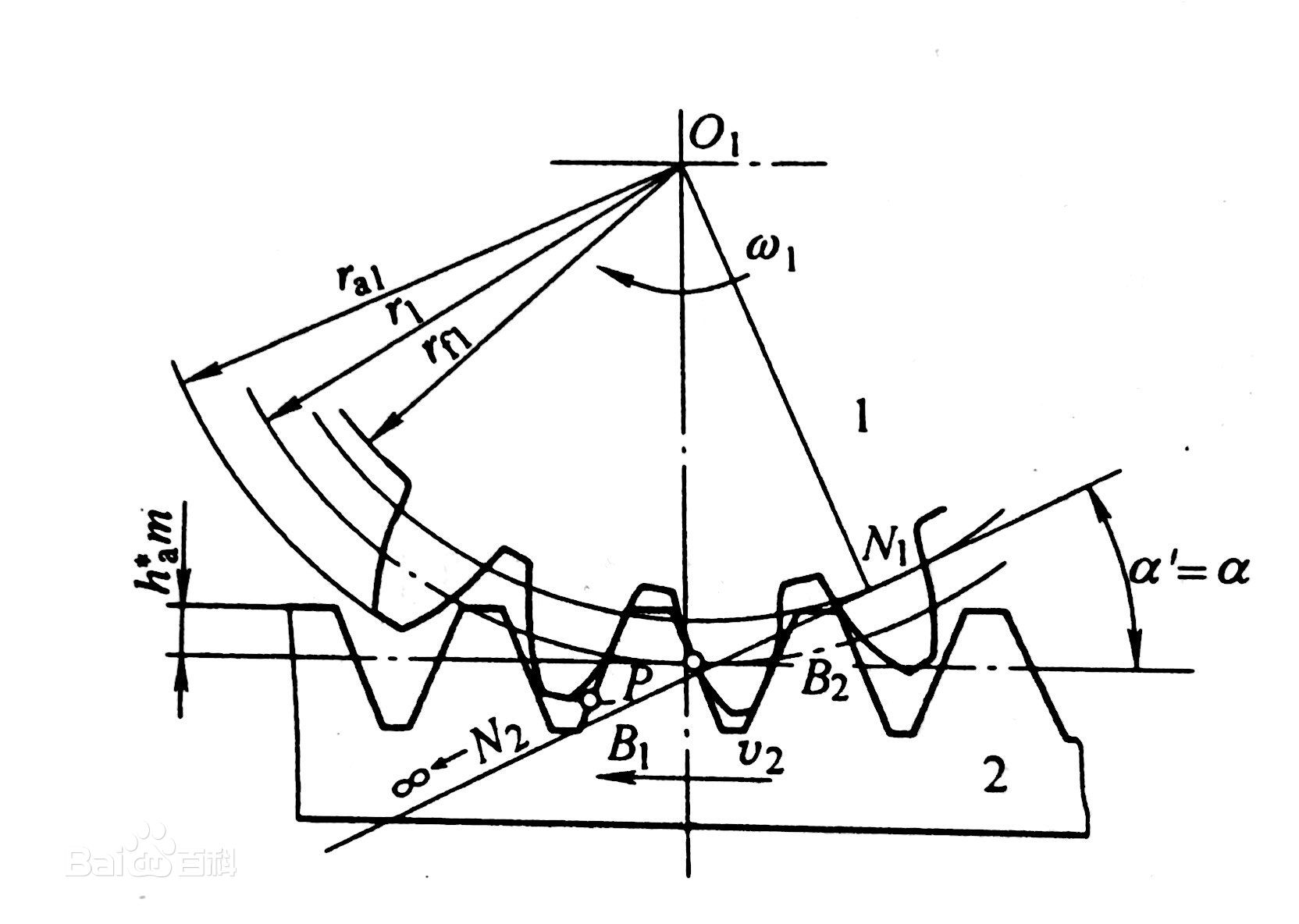
圖3 齒輪齒條傳動
圖3 齒輪齒條傳動圓柱直齒輪內嚙合傳動
兩齒輪內嚙合傳動時，其標準中心距為：
a=r2-r1=m(z2-z1)/2
（1）當按標準中心距安裝時，情況和圓柱直齒輪外嚙合相同。
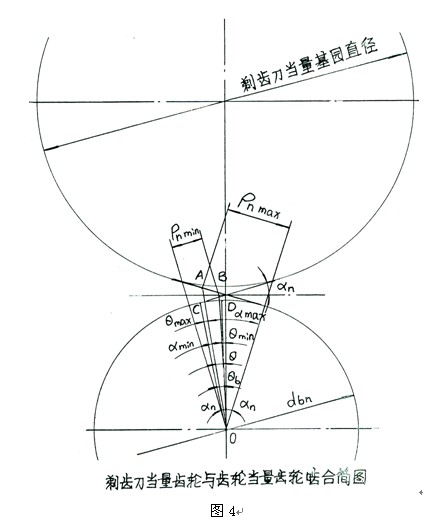
（2）當兩圓分度圓分離時，即其實際中心距小於標準中心距時，其漸近角將小於分度圓壓力角。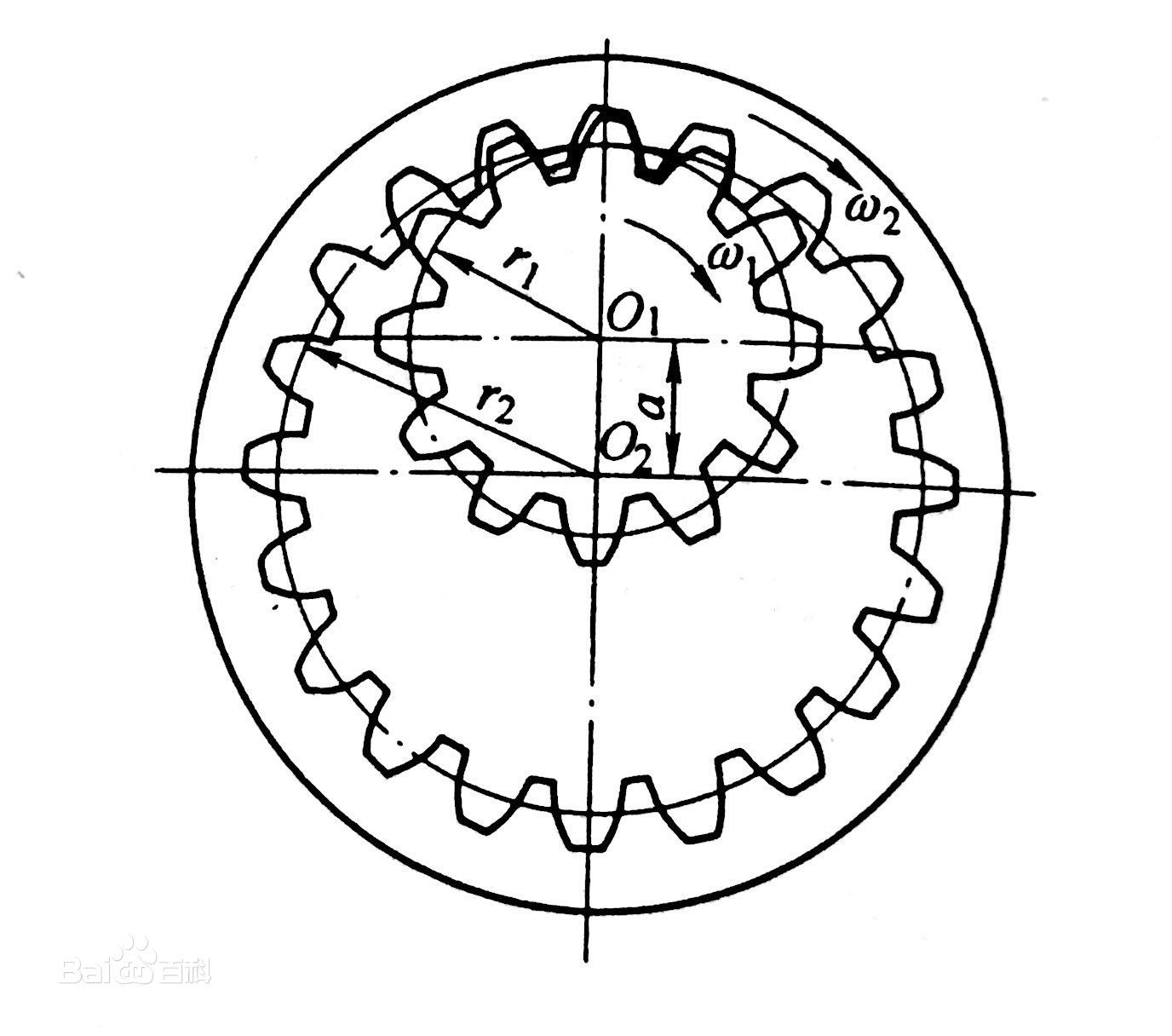
圖4 內嚙合傳動
圖4 內嚙合傳動斜齒圓柱齒輪傳動
斜齒輪的螺旋角β如圖5所示。
兩斜齒輪見的嚙合是由輪齒的一端進入嚙合逐漸過渡到另一端而最終退出嚙合。故斜齒輪的漸近角為螺旋角β。
一對斜齒輪正確嚙合的條件是：
（1）模數和壓力角相等（mn1=mn2，αn1=αn2）
（2）螺旋角滿足以下條件：
外嚙合：β1=-β2
內嚙合：β1=β2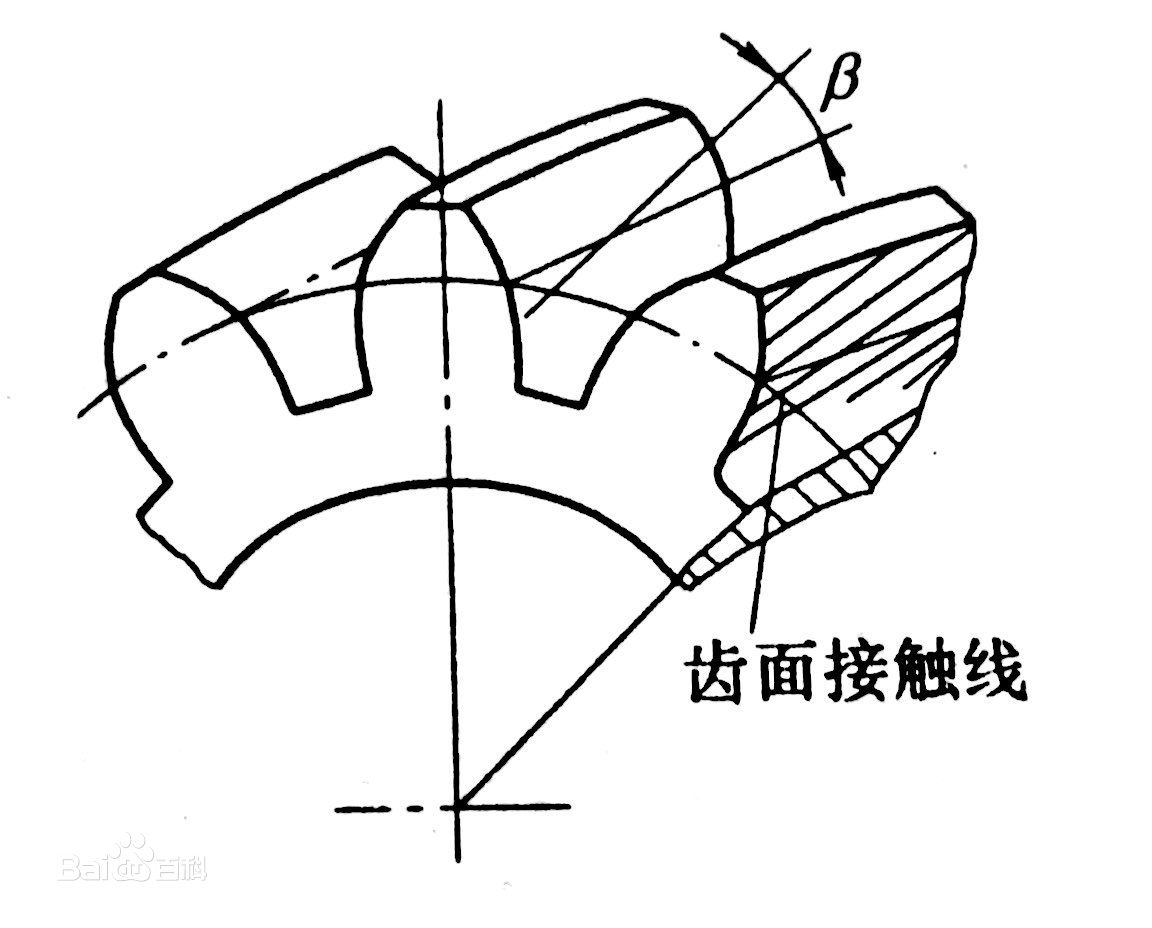
圖5 斜齒輪的螺旋角
圖5 斜齒輪的螺旋角直齒錐齒輪傳動
如圖6所示，兩個直齒錐齒輪傳動時，δ1、δ2分別為兩錐齒輪的分度圓錐角（簡稱分錐角）。
當兩齒輪的軸交角∑=90時，δ1+δ2=90。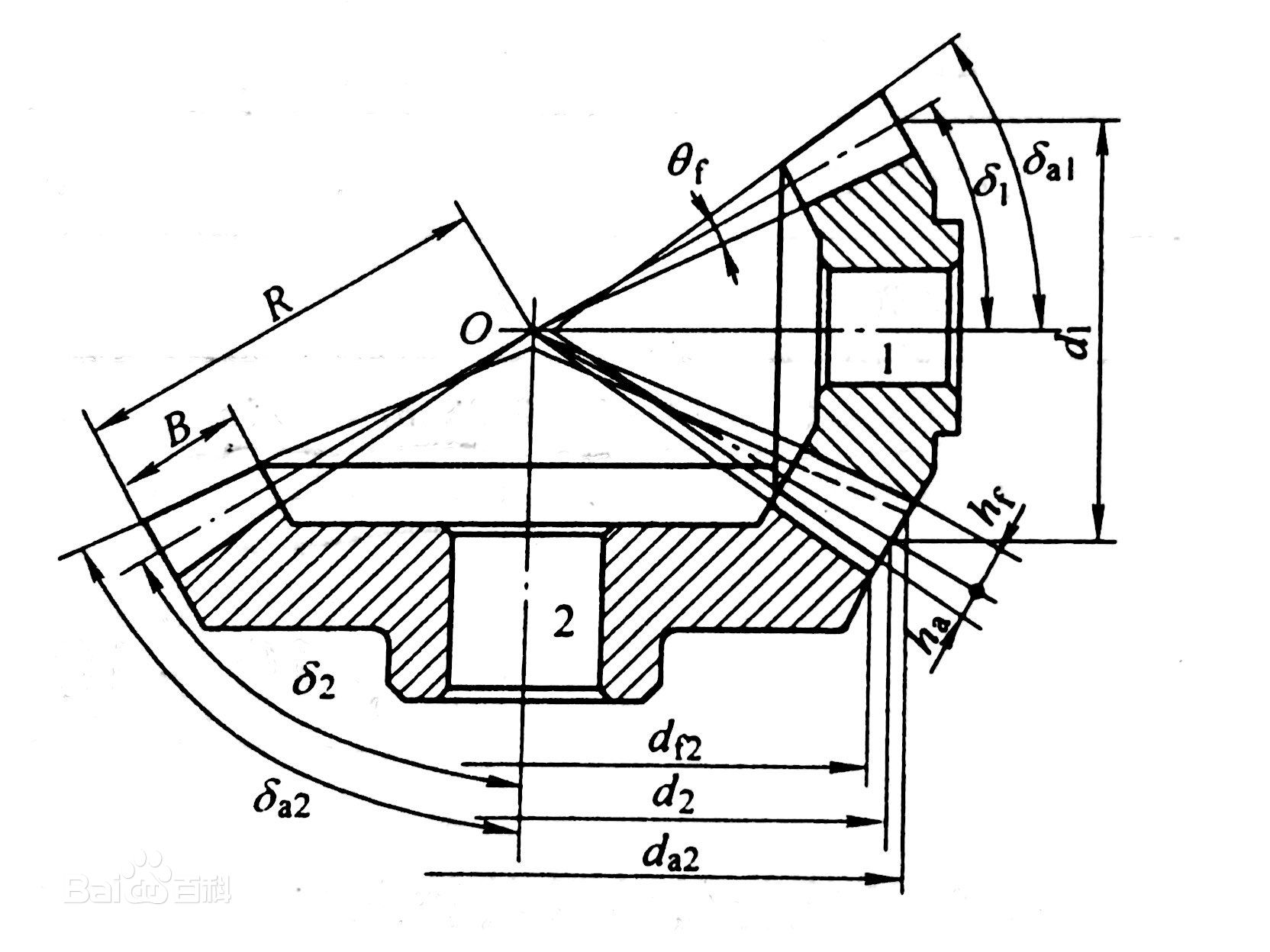
圖6 直齒錐齒輪傳動
圖6 直齒錐齒輪傳動渦輪蝸桿傳動
渦輪蝸桿正確嚙合的條件是：
（1）蝸桿的軸面模數mx1和壓力角αx1分別等於渦輪的端面模數mt2和壓力角αt2，且均取為標準值m和α，即：
mx1=mt2=m，αx1=αt2=α
（2）當蝸輪蝸桿的軸線交錯角∑=90時，還需保證γ1=β2，且兩者螺旋線旋向相同。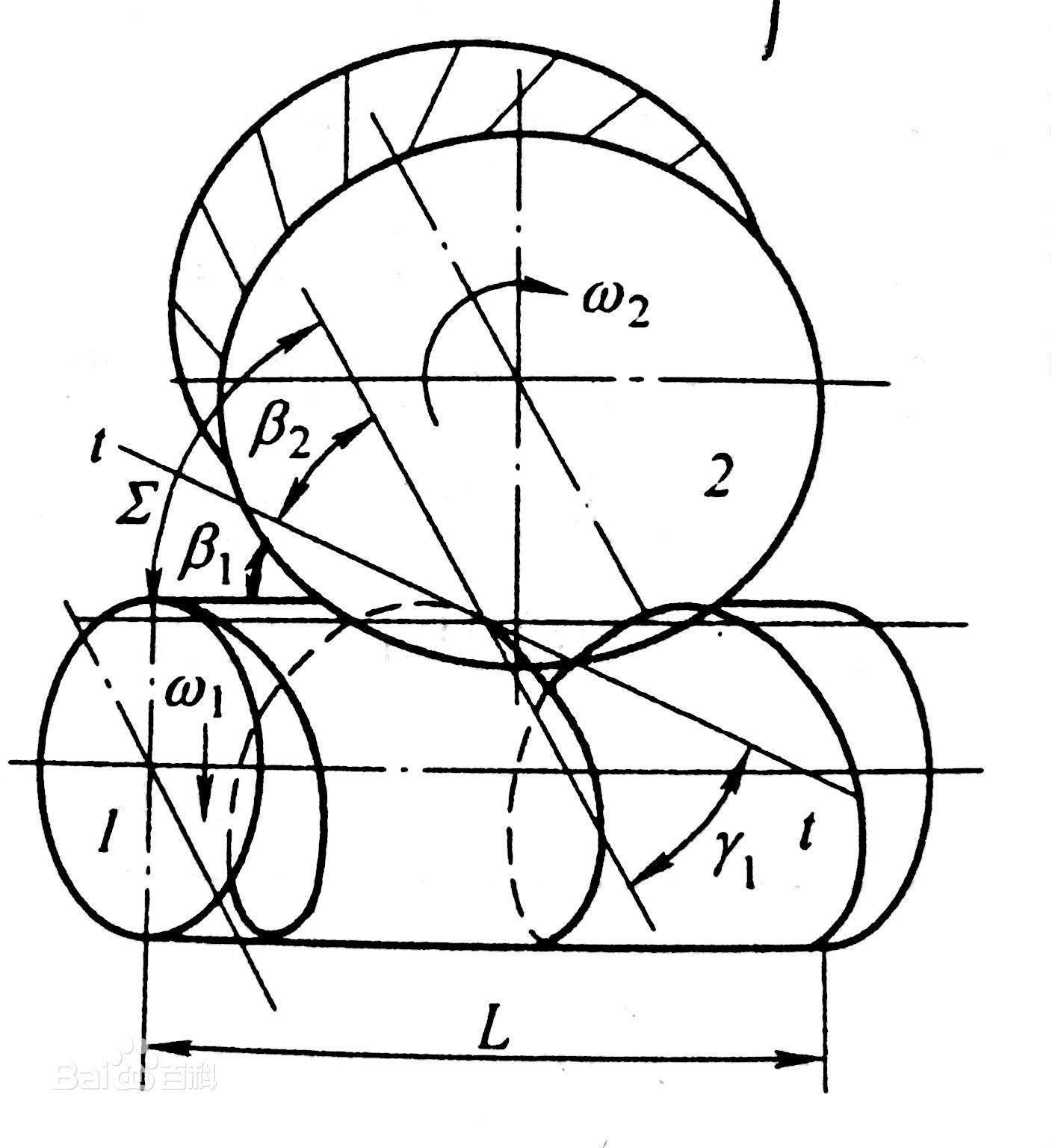
圖7 渦輪蝸桿傳動
圖7 渦輪蝸桿傳動相關概念
壓力角是指不計算摩擦力的情況下，受力方向和運動方向所夾的銳角。α是作用於C點的力F與點C速度方向之間所夾的銳角，則角α為該平面機構傳動時的壓力角，即F和Ft所夾的角。壓力角是判斷機構動力學性能的一個重要指標。
如圖所示，一對相嚙合漸開線齒輪的齒廓置E1和E2在任一點K接觸，齒輪1驅動齒輪2，兩輪的角速度分別為ω1和ω2。過K點作兩齒廓的公法線，由漸開線的性質可知，這條公法線必與兩輪基圓相切，即為兩輪基圓的內公切線，切點是N1和N2。當齒輪安裝完之後，兩輪的位置不再改變，兩基圓沿同一方向的內公切線只有一條，所以其內公切線N1N2與兩輪連心線O1O2必交於定點C這個定點稱為節點。以輪心為圓心，過節點所做的圓稱為節圓，兩輪節圓直徑分別用d1，和d2，表示。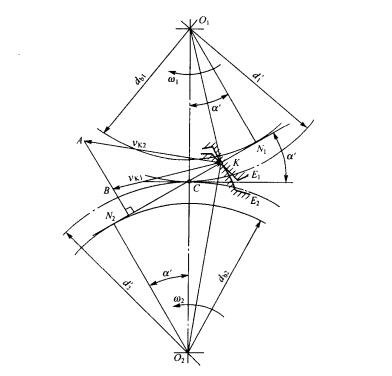
漸開線齒廓嚙合
漸開線齒廓嚙合