演化方程

演化方程(evolution equation)是揭示動態對策變化規律的方程。動態對策是與同步對策相對的概念，它意味著局中人按一定順序相繼作出若干步決策。對於動態對策通常考慮兩種均衡概念：子對策精練納什均衡與貝葉斯均衡。

基本介紹

• 中文名：演化方程
• 外文名：evolution equation
• 領域：數學
• 學科：博弈論
• 性質：揭示動態對策變化規律的方程
• 相關人物：貝葉斯

概念

演化方程是揭示動態對策變化規律的方程。即：

這裡考慮的是一個動態兩人零和對策：

式中X_k={x(k)}，Y_k={y(k)}分別表示局中人Ⅰ和局中人Ⅱ在k時刻的策略集，A_k是依賴於策略x(k)和y(k)的局中人Ⅰ的贏得函式，z(k)是狀態變數，f_k(·)是某個函式，當初態z(0)已知時，局中人Ⅰ在整個對策過程的贏得為

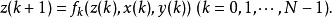
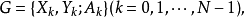
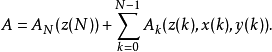
動態對策

動態對策是與同步對策相對的概念，它意味著局中人按一定順序相繼作出若干步決策。動態對策理論通常依賴於以下基本假設：

(1)每個局中人了解每一結局的後果，且確信其對手也了解這一點。

(2)每個局中人能完全記住自己及對手已 作出的所有策略選擇。

對於動態對策通常考慮兩種均衡概念：子對策精練納什均衡與貝葉斯均衡。

設對一展開型對策的每個決策結點x，指 定了機率μ(x)，使得對每個信息集H，有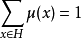 。對於信息集H、在H行動的局中人i及某個混合策略組σ=(σ_i，σ_-i)，若對i的任何其他混合策略_i，i在策略組(σ_i，σ_-i)下從H 開始的期望收益不小於在(_i，σ_-i)下從H開始的期望收益，即：E[u_i|H，μ，σ_i，σ_-i]≥E[u_i|H，μ，_i，σ_-i]，則說σ對H是序列合理的。若σ對所有信息集 H是序列合理的，且當P_rob(H |σ)>0時，對任何x∈H有：P_rob(x|σ)=μ(x)P_rob(H|σ)，則稱σ為弱完全貝葉斯均衡，簡稱為WPBE。 WPBE必為納什均衡，反之則未必。

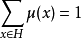
貝葉斯均衡

貝葉斯均衡是不完全信息博弈(貝葉斯博弈)的均衡概念，靜態的不完全信息博弈的均衡被稱為貝葉斯納什均衡，動態的不完全信息博弈的均衡被稱為精煉的貝葉斯納什均衡。解決不完全信息的方法是使用哈薩尼轉換。

靜態貝葉斯博弈記為G={a₁，…，a_n;θ₁， …，θ_n;p₁，…，p_n;u₁，…，u_n}。其中a_i是第i個博弈方採取的行動(純策略)，a_i∈A_i(θ_i)，A_i(θ_i)是 第i個博弈方類型依存的行動空間；θ_i是第i個博弈方的類型，Θ_i是第i個博弈方的類型空間；p_i是第i個博弈方的類型為θ_i(θ_i∈Θ_i)的機率。 u_i是第i個博弈方的效用，u_i=u_i(a₁，…，a_i，…， a_n;θ₁，…，θ_i，…，θ_n)=u_i(a_i，a_-i;θ_i，θ_-i)。其中θ_-i=(θ₁，…，θ_i-1，θ_i+1，…，θ_n)。

定義一：如果對所有的i，a_i*∈A_i(θ_i)，使得：

則a^*=(a₁^*，…，a_n^*)就稱為一個(純策略)貝葉斯納什均衡。混合策略的貝葉斯納什均衡的定義類似。其中p_i(θ_-i|θ_i)是第i個博弈方在已知 自己的類型為θ_i時判定其他博弈方類型屬於θ_-i的機率。

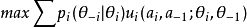
在動態博弈中，記S_i(θ_i)為第i個博弈方類 型依存的策略空間，s_i∈S_i(θ_i)是S_i中的一個特 定的策略。記a_-i^h=(a₁^h，…，a_i-1^h，a_i+1^h，…，a_n^h)是 在第h個信息集上參與人i觀測到其他參與人的行動組合。記p(θ_-i|a_-i)是第i 個博弈方在觀測到a_-i後關於θ_-i的後驗機率。

定義二：精煉貝葉斯均衡是一個策略組合 s^*=(s₁^*，…，s_n^*)和一個後驗機率分布p=(p₁， …，p_n)，滿足：

1.對於所有博弈方i，在每一個信息集h，s_i^*使得：

2.後驗機率_i(θ_-i|a_-i)是使用貝葉斯法則，從先驗機率p_i(θ_-i|θ_i)，觀察到的a_-i和最優 策略s_-i得到的(在可能的情況下)。

需要注意的是，精煉的貝葉斯均衡不僅僅是關於策略的均衡，而是關於策略s和對類型的判斷(信念)的共同均衡。 給定信念p，策略s是最優的;給定均衡策略s，是使用貝葉斯法則從均衡策略和觀測到的行動得到的。

貝葉斯博弈

又稱“不完全信息博弈”。“完全信息博弈”的對稱。至少有一個參與者不知道其他參與者的類型特徵、對策和收益的一種博弈類型。不完全信息博弈是以英格蘭機率統計學家貝葉斯(Bayes，Thomas，1702—1761)的名字命名的。

1967年前，博弈論對不完全信息博弈是無能為力的。匈牙利經濟學家海爾薩尼(Harsanyi，John Charles， 1920—2000)引入了虛擬參與者——“自然”，將不完全信息模型化並進行分析。其工作被稱為“海爾薩尼轉換”。通過這個轉換，海爾薩尼將不完全信息博弈轉換為完全但不完美信息博弈。所謂不完美信息博弈，是指“自然”作出了它的選擇，但是其他參與者並不知道它的具體選擇是什麼，僅知道該選擇的各種可能的機率分布(先驗信念)。在這個基礎上，海爾薩尼定義了“貝葉斯-納什均衡”(或稱為“貝葉斯均衡”)。貝葉斯均衡是納什均衡在不完全信息博弈中的擴展。

子對策精練納什均衡

設Γ是有N個局中人的展開型對策。Γ的 一個子集G稱為Γ的一個子對策，若它滿足以 下兩個條件：

(1)G從某個含惟一決策結點的信息集開始，包含這個結點的所有(直接或間接)後繼決 策結點，且僅含有這樣的結點。

(2)G由若干完整的信息集組成，即若G含信息集H中某點x，則必定包含整個H。

子對策自身組成一個對策，因而可對之套用對策論的結論。

給定Γ的子對策G與Γ的納什均衡σ。若 當G單獨考慮時，σ對應G中信息集的那些行為構成G的一個納什均衡，則說σ在子對策G 中導出一個納什均衡。若σ在Γ的每個子對策 中導出一個納什均衡，則稱σ為Γ的子對策精 練納什均衡，簡稱為SPNE。SPNE必定是納什 均衡，但反之則未必，試看下例。

設Γ是如下圖所示的展開型對策。開發商 A的策略集S_A={開發，不開發}；B的策略集

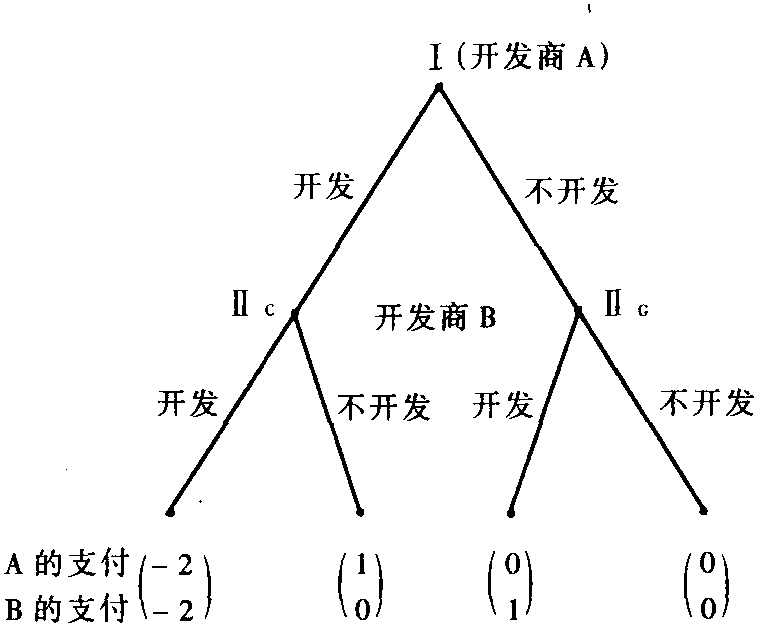
S_B={(開發，開發)，(開發，不開發)，(不開發， 開發)，(不開發，不開發)}，其中(開發，開發)表 示策略“當A開發時B開發，當A不開發時B 開發”，其餘類推。Γ可表示如下表所示的標準 型對策。這個標準型對策有三個納什均衡：

(開發，(不開發，開發))、(開發，(不開發，不開 發))與(不開發，(開發，開發))。對策Γ有三個 子對策：Γ本身及分別從結點Ⅱ_C與Ⅱ_G出發的 子對策C與G。因在子對策C內不開發是最優的，而在子對策G內開發是最優的，故(開發， (不開發，開發))分別在C與G內考慮時是納 什均衡，從而它是SPNE。但易於驗證，P的其 他兩個納什均衡都不是SPNE。