在高能中微子與夸克或核子的相互作用中,其散射截面因產物不同而與這兩種角有不同的關係。其中,當產物中有帶電荷的輕子時,散射截面都與卡比坡角的正弦平方或餘弦平方有關:當產物中只有中微子時,散射截面則與溫伯格角的正弦平方有關。
基本介紹
- 中文名:溫伯格角
- 外文名:Weinberg angle
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:粒子
- 同類:卡比坡角
概念,基本原理,
概念
如果我們構想由基態基本子構成的真空點陣是像氯化鈉晶體那樣的立方點陣,當做為陣點的基態基本子激發而使真空單胞變成粒子時,單胞的對稱性也要發生變化。因為正如由原子或離子構成的晶體,當原子或離子的種類變化如原子或離子的體積變化時,也會引起晶體對稱性的變化,甚至從一種晶系變為另一種晶系。基態基本子和激發態基本子不但質量-能量相差很大,體積的變化也應很大,因為這樣微小的粒子的大小是可以用其德布羅意波長來估計的。由於德布羅意波長與粒子的能量關係如下:
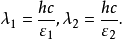

 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
如果用這個比值估計兩個基本子大小的比值,則可從表1看到,基態基本子和激發態基本子的大小相差懸殊。
計算表1時,除了採用表1的數據外,還取基態基本子的能量分別為
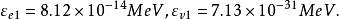
顯而易見,構成真空單胞的基態基本子的激發,應引起真空單胞的某種變化,如單胞體積的變化、對稱性的變化等。如果用晶體類比,構成晶體的原子或離子變化時,會司引起晶體點陣單胞的大小和對稱性變化。
眾所周知,在粒子物理中本來就有這樣的類比:認為卡比坡角或溫伯格(StevenWeinberg,1933~)角類似於晶體中的光學角度。例如,在高能中微子與夸克或核子的相互作用中,其散射截面因產物不同而與這兩種角有不同的關係。其中,當產物中有帶電荷的輕子時,散射截面都與卡比坡角的正弦平方或餘弦平方有關:當產物中只有中微子時,散射截面則與溫伯格角的正弦平方有關。
這些事實表明,如果把卡比坡角和溫伯格角看成是真空單胞激發時對稱性變化的一種表現,有如晶體光學角度的變化,那么,我們就可以更直觀地討論相應的問題。
基本原理
關於溫伯格角 的物理意義,可以形象地說明如下:在格拉肖-溫伯格-薩拉姆理論提出之前,電磁作用和弱作用的理論是分別獨立的,其有關參量如表2所示。
的物理意義,可以形象地說明如下:在格拉肖-溫伯格-薩拉姆理論提出之前,電磁作用和弱作用的理論是分別獨立的,其有關參量如表2所示。

場 | 耦合常數 | 場的流 | 場量子 |
電磁作用 |  |  |  |
弱作用 |  |  | 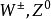 |
表2中電磁作用耦合常數 和弱作用耦合常數
和弱作用耦合常數 之間無聯繫。
之間無聯繫。




場 | 耦合常數 | 場的流 | 場量子 | |
弱電統一場  | 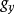 |  |  |  |
 |  |  | ||
描寫弱、電統一的流是 和
和 ,傳遞量子為
,傳遞量子為 ,
, ,
, 和
和 (可重新組合成
(可重新組合成 、
、 和
和 ),而弱電統一的耦合常數為
),而弱電統一的耦合常數為 和
和 。
。











表2中的耦合常數 和
和 (可以直接測量)與表3中的耦合常數
(可以直接測量)與表3中的耦合常數 和
和 (不能直接測量)之間的關係可用圖1表示。
(不能直接測量)之間的關係可用圖1表示。




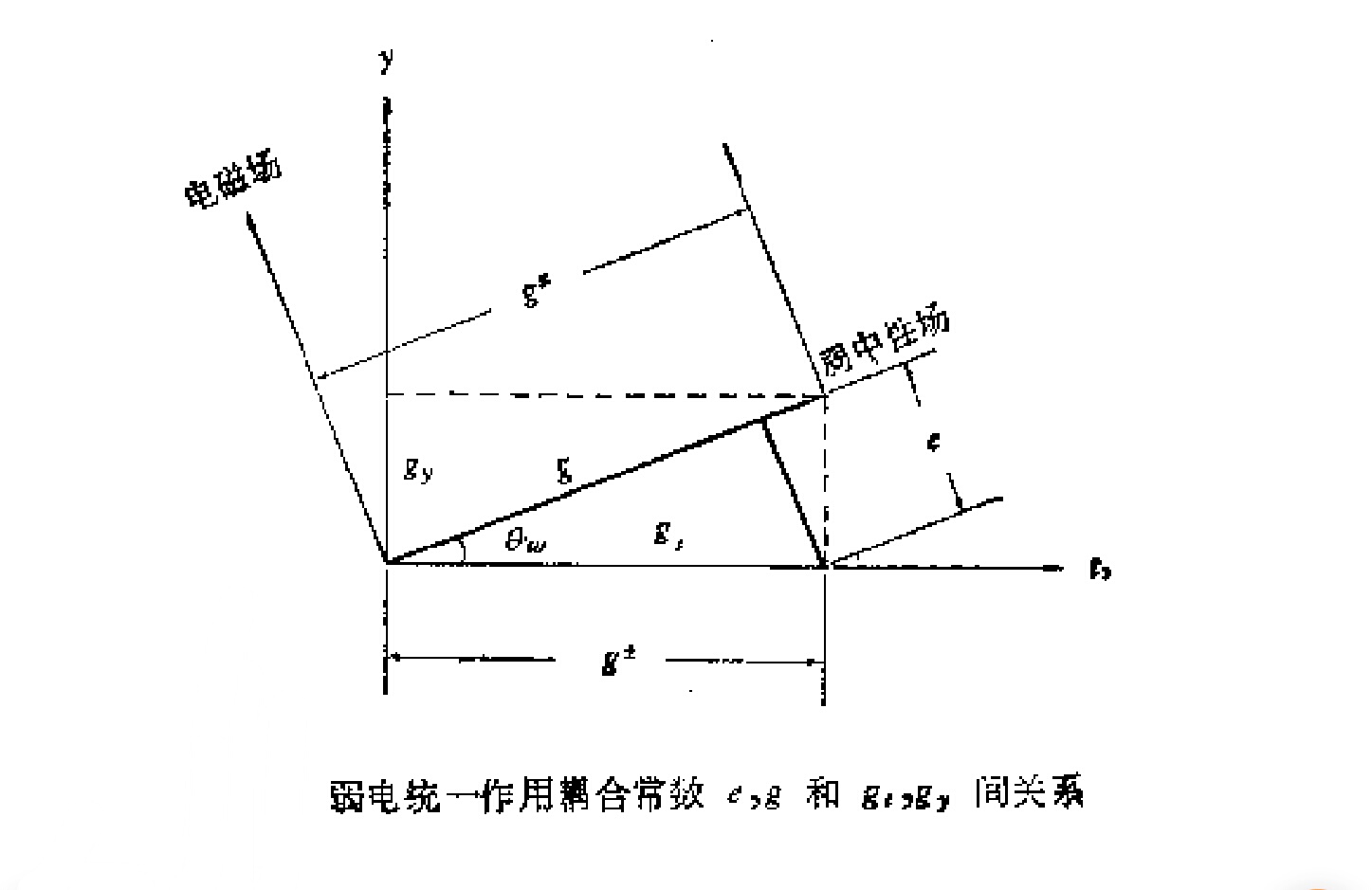
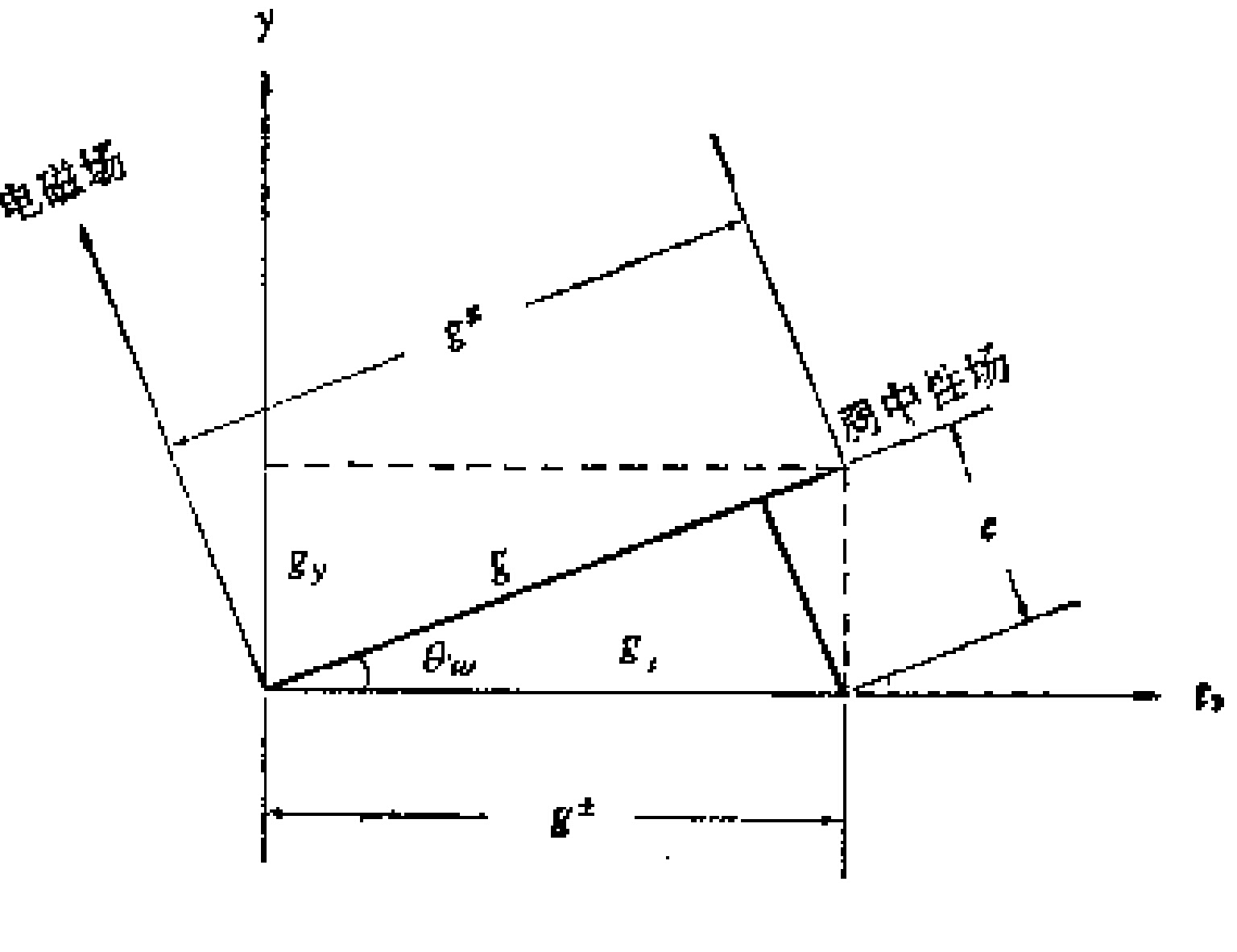 圖1
圖1圖1中以 、
、 代表弱電統一理論的兩個軸,基本耦合常數
代表弱電統一理論的兩個軸,基本耦合常數 在
在 和
和 兩軸上的投影分別為
兩軸上的投影分別為 和
和 ,
,










取弱中性耦合常數 ,弱帶電耦合常數
,弱帶電耦合常數 ,電磁場與弱中性場的一組軸和以
,電磁場與弱中性場的一組軸和以 、
、 軸相對旋轉角
軸相對旋轉角 .由圖4可知
.由圖4可知 是
是 的二次投影,即
的二次投影,即












由此可見, 實際上是連續兩類耦合常數的一個參量,也是連續弱作用和電磁作用耦合常數的一個參量。
實際上是連續兩類耦合常數的一個參量,也是連續弱作用和電磁作用耦合常數的一個參量。