準隨機數發生器(QRNG)產生高度均勻的單位超立方體樣本。 QRNG最小化生成點的分布與超立方體的統一分區的每個子立方體中具有相等比例點的分布之間的差異。 因此,QRNG系統地填充所產生的準隨機序列的任何初始段中的“空穴”。
基本介紹
- 中文名:準隨機數
- 外文名:Quasi-Random Numbers
- 英文縮寫:QRNG
- 隨機數:真隨機數、準隨機數、偽隨機數
- 產生:高度均勻的單位超立方體樣本
- 領域:機器學習;人工智慧
概念,QRNG套用,準隨機點集,生成準隨機點集,準隨機流,
概念
準隨機數發生器(QRNG)產生高度均勻的單位超立方體樣本。 QRNG最小化生成點的分布與超立方體的統一分區的每個子立方體中具有相等比例點的分布之間的差異。 因此,QRNG系統地填充所產生的準隨機序列的任何初始段中的“空穴”。
與普通偽隨機數生成方法中描述的偽隨機序列不同,準隨機序列在許多隨機性的統計檢驗中失敗了。 然而,近乎真實的隨機性並不是他們的目標。 準隨機序列尋求均勻填充空間,並以這樣的方式進行,使得初始段近似該行為直到指定的密度。
QRNG套用
(1)準蒙特卡羅(QMC)整合。
蒙特卡羅技術經常用於評估困難的多維積分,而無需封閉形式的解決方案。 QMC使用準隨機序列來改善這些技術的收斂性質。
(2)空間填充實驗設計。
在許多實驗設定中,在每個因素設定下進行測量是昂貴的或不可行的。 準隨機序列為設計空間提供了有效、均勻的採樣。
(3)全局最佳化。
最佳化算法通常在初始值附近找到局部最優值。 通過使用初始值的準隨機序列,搜尋全局最優值對所有局部最小值的吸引盆地進行均勻採樣。
準隨機點集
統計和機器學習Toolbox™中有生成準隨機序列的函式:
(1)哈爾頓序列。
由haltonset功能產生。 這些序列使用不同的基數來形成每個維度中單位間隔的相繼更好的均勻分區。
(2)Sobol序列。
由sobolset功能產生。 這些序列使用2的基數來形成相繼更精細的單位間隔的均勻分區,然後重新排列每個維度中的坐標。
(3)拉丁超立方體序列。
由lhsdesign功能製作。 儘管在最小化差異的意義上不是準隨機的,但是這些序列仍然產生在實驗設計中有用的稀疏均勻樣本。
準隨機序列是從正整數到單位超立方體的函式。為了在套用中有用,必須生成序列的初始點集。點集是大小為n-by-d的矩陣,其中n是點的數量,d是被採樣的超立方體的維度。函式haltonset和sobolset構造具有指定準隨機序列屬性的點集。點集的初始段由qrandset類(haltonset類和sobolset類的父類)的net方法生成,但可以使用括弧索引更一般地生成和訪問點。
由於產生準隨機序列的方式,它們可能包含不期望的相關性,特別是在其初始段中,特別是在較高維度。為了解決這個問題,準隨機點集經常跳過,跳過或擾亂序列中的值。 haltonset和sobolset函式允許您指定準隨機序列的跳過和跳躍屬性,而qrandset類的加擾方法允許您套用各種加擾技術。加擾減少了相關性,同時也提高了均勻性。
生成準隨機點集
下面例子顯示了如何在MATLAB中嘗試使用haltonset來構建一個2-D Halton準隨機點集。
創建一個haltonset對象p,它跳過序列的前1000個值,然後保留每101個點。
rng default % For reproducibilityp = haltonset(2,'Skip',1e3,'Leap',1e2)
p =
Halton point set in 2 dimensions (89180190640991 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : none
對象p封裝指定的準隨機序列的屬性。 點集是有限的,其長度由跳過和跳躍屬性確定,並且由點集索引的大小限制。
使用加擾來運用反向加擾。
p = scramble(p,'RR2')
p =
Halton point set in 2 dimensions (89180190640991 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : RR2
使用網路生成前500個點。
X0 = net(p,500);
等效於
X0 = p(1:500,:);
點集X0的值不會生成並存儲在記憶體中,直到使用網路或括弧索引訪問p。
為了詮釋準隨機數的性質,用X0創建二維的散點圖。
scatter(X0(:,1),X0(:,2),5,'r')axis squaretitle('{\bf Quasi-Random Scatter}')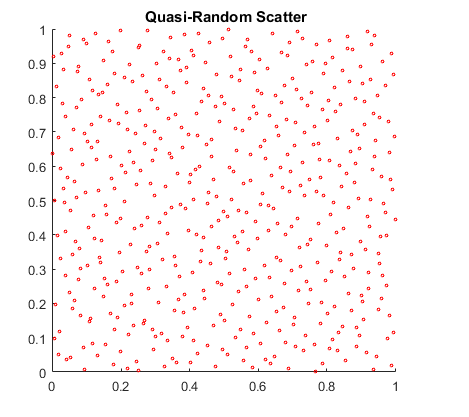
將其與由rand函式生成的均勻偽隨機數的散點進行比較。
X = rand(500,2);scatter(X(:,1),X(:,2),5,'b')axis squaretitle('{\bf Uniform Random Scatter}')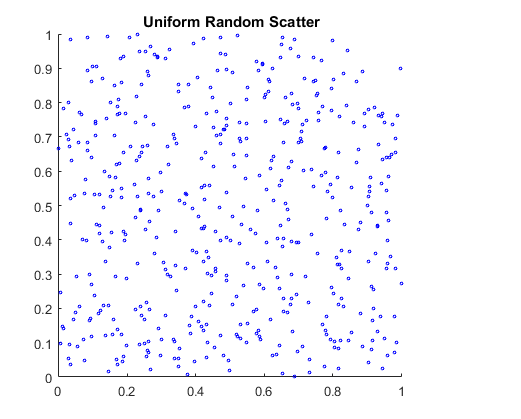
準隨機散射看起來更均勻,避免了偽隨機散射中的聚集。
在統計意義上,準隨機數太均勻,不能通過傳統的隨機測試。 例如,由kstest執行的Kolmogorov-Smirnov測試用於評估點集是否具有均勻的隨機分布。 在統一的偽隨機樣本(如rand所產生的樣本)上重複執行時,測試產生均勻的p值分布。
nTests = 1e5;sampSize = 50;PVALS = zeros(nTests,1);for test = 1:nTests x = rand(sampSize,1); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval;endhistogram(PVALS,100)h = findobj(gca,'Type','patch');xlabel('{\it p}-values')ylabel('Number of Tests')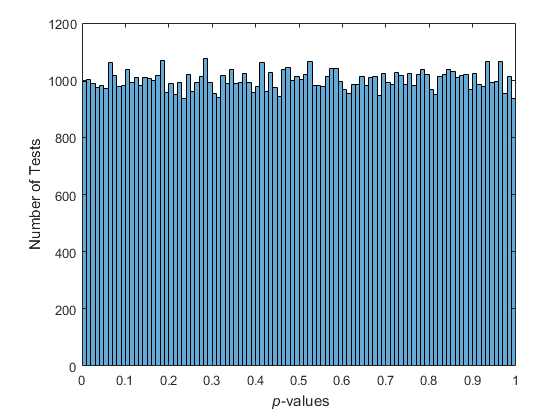
當在均勻的準隨機樣本上重複執行測試時,結果是完全不同的。
p = haltonset(1,'Skip',1e3,'Leap',1e2);p = scramble(p,'RR2');nTests = 1e5;sampSize = 50;PVALS = zeros(nTests,1);for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval;endhistogram(PVALS,100)xlabel('{\it p}-values')ylabel('Number of Tests')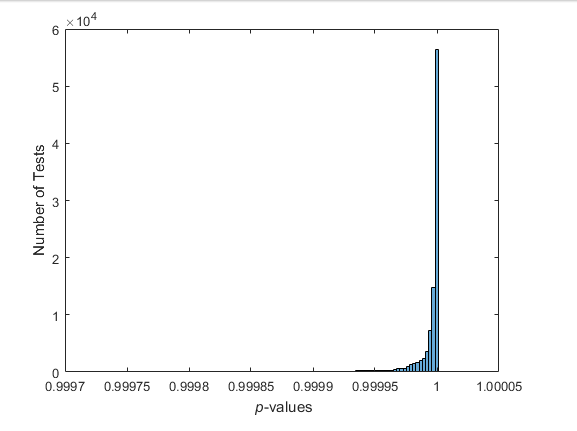
小的p值引起了數據均勻分布的零假設的質疑。如果這個假設是真實的,那么約有5%的p值預計會低於0.05。
準隨機流
由qrandstream函式產生的準隨機流用於生成順序準隨機輸出,而不是特定大小的點集。如pseudoRNGS,當客戶端應用程式需要可以間歇訪問的無限大小的準隨機數的來源時。 當構建流時,設定準隨機流的屬性,例如其類型(Halton或Sobol)、維度、跳過、跳躍和加擾。
在實現中,準隨機流本質上是非常大的準隨機點集,儘管它們被不同地訪問。 準隨機流的狀態是要從流中獲取的下一個點的標量索引。 使用qrandstream類的qrand方法從當前狀態開始從流中生成點。 使用reset方法將狀態重置為1與點集不同,流不支持括弧索引。
生成準隨機流
使用haltonset創建準隨機點集p,然後將索引重複增加到點集測試中以生成不同的樣本。
p = haltonset(1,'Skip',1e3,'Leap',1e2);p = scramble(p,'RR2');nTests = 1e5;sampSize = 50;PVALS = zeros(nTests,1);for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval;end
通過使用qrandstream基於點集p構造準隨機流q並使流處理到索引的增量來獲得相同的結果。
p = haltonset(1,'Skip',1e3,'Leap',1e2);p = scramble(p,'RR2');q = qrandstream(p);nTests = 1e5;sampSize = 50;PVALS = zeros(nTests,1);for test = 1:nTests X = qrand(q,sampSize); [h,pval] = kstest(X,[X,X]); PVALS(test) = pval;end
