湍流的起因 層流過渡為湍流的主要原因是不穩定性。在多數情況下,剪下流中的擾動會逐漸增長,使流動失去穩定性而形成湍流斑,擾動繼續增強,最後導致湍流。這一類湍流稱為剪下湍流。兩平板間的流體受下板面加熱或由上板面冷卻達到一定程度,也會形成流態失穩,猝發許多小尺度的對流;上下板間的溫差繼續加大,就會形成充分發展的湍流。這一類湍流稱
熱湍流 或對流湍流。
邊界層 、
射流 以及管道中的湍流屬於前一類;夏天地球大氣受下墊面加熱後產生的流動屬於後一類。
為了弄
清湍 流過渡的機制,科學家們開展了關於流動穩定性理論(見
流體運動穩定性 )、分岔(bifurcation)理論和
混沌 (chaos)理論的研究,還進行了大量實驗研究(見
湍流實驗 )。
對於從下加熱流層而向湍流過渡的問題,原來傾向於下述觀點:隨著流層溫差的逐漸增加,在發生第一不穩定後,出現分岔流態;繼而發生第二不穩定,流態進一步分岔;然後第三、第四以及許多更高程度的不穩定接連發生;這種複雜的流動稱為湍流。實驗結果支持這一論點。但是,這一運動過程在理論上得不出帶有連續譜的無序運動,而與實驗中觀察到的連續譜相違。對不穩定系統的理論分析提出了另一種觀點:在發生第一、第二不穩定之後,第三不穩定就直接導致一個可解釋為湍流的無序運動。這一觀點也得到實驗的支持。
剪下流中湍流的發生情況更為複雜。實驗發現,平滑剪下流向湍流過渡常會伴有突然發生的、作奇特波狀運動的湍流斑或稱過渡斑。可以構想,許多逐漸形成的過渡斑,由於一再出現的新的突然擾動而互相作用和衰減,使混亂得以維持。把過渡斑作為一種孤立的非線性波動現象來研究,有可能對湍流過渡現象取得較深刻的理解。因此,存在著不止一條通向湍流的途徑。
過去認為,一個機械系統發生無序行為往往是外部干擾或外部噪聲影響的結果。然而,觀察到:在某個系統里進行確定的基本操作會導致混亂的重複發生。這類系統可認為含有一個能吸引系統維持混亂的奇怪吸引子。這種混亂現象稱為短暫混沌。預期對這種短暫混沌的可普遍化特性的研究將會得到說明完全發展的無序現象(湍流)的新線索。
湍流的基本方程 充分發展的湍流流動圖像極其複雜,雖經一百多年的研究,成果並不顯著。大多數學者都是從
納維-斯托克斯方程 出發進行研究;有人從統計物理學中的
玻耳茲曼方程 或BBGKY譜系方程出發進行研究。
對充分發展的湍流,除考慮它的瞬時量外,更要考慮各種用以描述湍流概貌的平均量。從瞬時量導出平均量的平均方法有好多種。有了平均法,就可把任一瞬時量分解成平均量和脈動量之和。例如,
ui=ūi+u′i,p=pˉ+p′,
式中ui、p為速度和壓力的瞬時量;ūi、pˉ圴為其平均量;u′i和p′為其脈動量。對式(1)取平均,就得到平均速度和平均壓力所滿足的雷諾方程:
式中最後一項是雷諾方程對納維-斯托克斯方程的附加項,體現了脈動場對平均場的作用,。式中最後一項中的量實質上是新未知量,所以式(2)和連續性方程
所組成的方程組關於ū
i 和pˉ圴是不封閉的,因而無法求解。學者們一直努力尋求封閉方程組的辦法;早年的
普朗特混合長理論 是一種嘗試,後來發展的模式理論也是一種嘗試。
湍流的半經驗理論和模式理論 J.V.布森涅斯克早在1877年作出假設:二元湍流的雷諾應力正比於平均速度梯度,即
式中ε
τ 為渦粘性係數。這一假設是仿照牛頓粘性定律作出的。實際上,ε
τ 不是單由物性決定的常數,而是和流動有關的變數,尤其在近壁區,它的變化很大。後來,
L.普朗特 仿照氣體分子運動論,提出了混合長理論,即令
式中取x、y坐標;u′、v′為相應脈動速度分量;
l 稱為混合長。根據平板邊界層的測量,
l 和離壁之距y的關係可近似地表示為:
式中yc=0.15δ~0.20δ;κ=0.40;σ=0.075~0.09;δ為邊界層厚度。對於二元混合層和射流,l 近似地和射流的寬度成比例。在二元情況下可用式(4)封閉式(2)、(3)。
對於直圓管湍流,由混合長理論可以得出用對數函式近似表示的水桶型的速度分布。經過實驗修正後,這個
對數分布 律為:
除了混合長理論外。G.I.泰勒提出過一種模擬渦量輸運的理論;T.von卡門也提出一種假定局部脈動場相似的理論。有人稱這些半經驗理論為平均場封閉模式或“0”方程模式。這種模式比較簡單,且計算結果也比較符合某些工程實際。
上述半經驗理論是近似的,適用範圍有限。後來,經過改進和推廣,出現了“1”方程模式,其中除了平均運動方程外,還補充一個湍能方程或一個關於混合長的微分方程;還有所謂“2”方程模式和應力輸運模式,以及更高階的封閉模式。
式中μt =Cμ ρK2 /ε,Cμ 為比例常數。再對K和ε分別補充一個方程,就可組成同時計算平均速度場和湍流場的封閉方程組。K-ε模式已用於計算一些平面平行湍流,但計算稍為複雜的湍流時,效果不好。
應力輸運模式用六個關於雷諾應力分量的輸運方程增補方程(2)、(3),並引進一些附加假定。
周培源 早在1945年發表了他對應力輸運模式較系統的研究工作,當時沒有電子計算機,只能作一般性討論。從60年代起開始套用計算機研究這一模式。在應力輸運模式中,湍流的脈動場用七個量(六個雷諾應力分量和一個耗散率)描寫,比只用K和ε兩個量似乎合理些,但同樣存在封閉的困難。因耦合的方程數目增多,對邊界條件和初始條件的要求也增多,從而給計算帶來許多困難。
上述兩種二階封閉都立足於雷諾平均法則,湍流場被分解為平均場和脈動場。脈動場由u
' i u
k '― 和ε來代表中既有大渦的作用,u
' i u
' k 也有小渦的作用,也就是把脈動場中的大渦和小渦同等看待,這可能是造成封閉方程組過分複雜的原因。此外,雷諾平均法則不能反映一些擬序性的大渦結構。為此,又開始探索新的平均方法和封閉模式。“濾波”平均(即將小渦濾去)和大渦模擬就是這一方面的嘗試。
還有和封閉理論相反的、被稱為開式理論的方法。它不是用假設來截斷一連串的方程,而是在許多可能的解中尋求給出某些重特要征的上界的解。
上述模式理論和半經驗理論都是對非均勻湍流作定量的預估,尋求用一個簡單的統計模式來代替複雜的實際過程,以預測各種工程的或其他實用場合中的湍流特性。
湍流的統計理論 研究湍流一般要用統計平均概念。統計的結果是湍流細微結構的平均,描述流體運動的某些概貌,而這些概貌對實際湍流細節應該是適當敏感的,因此可以認為,幾乎所有湍流理論(包括上兩節所述的理論)都是統計理論,但一般著作中所講的統計理論實際上是指引進多點相關後的統計理論。
式中
稱為相關係數。知道了拉格朗日相關,就可以算出湍流擴散係數。1935年泰勒又引進同一時刻不同點上速度分量的相關,用以描述湍流脈動場,此即所謂歐拉相關。相應的相關係數
泰勒利用這一類相關研究了一種理想湍流──均勻各向同性湍流。這種量簡單的理想化湍流的定義是:平均速度和所有平均量都對空間坐標的平移保持不變,而且各相關函式沿任何方向都是相同的。要在實驗室中即使近似地模擬這種湍流也是很困難的。但在這種湍流中,不會有平均流動對脈動的互動作用,也不會有因不均勻性造成的湍能擴散效應和因各向異性造成的湍能重分配效應,因而可以利用這種湍流研究湍能衰減規律和湍流場中各級旋渦間的能量分配和交換規律。由於沒有湍能產生和擴散,這種湍流一旦產生就逐漸衰減。泰勒導得湍能的衰減律為:
式中λ為湍流的泰勒微尺度;u為脈動速度。這種湍流的所有二階速度相關可以由一個縱向相關函式表示
式中
l 表示P點和P′點間連線的方向;r為兩點間的距離;u
l (0)、u'
l (r)分別為P點和P
' 點上的脈動速度在
l 方向的分量;為
l 方向脈動速度的自相關,稱縱向自相關,它的1.5倍就是湍能。卡門和L.豪沃思導出關於f(r)的動力學方程:
式(7)稱為卡門-豪沃思方程,它描述相關隨時間的變化。解出f就可求出流場的衰減規律。把此方程按r的冪次展開,其第一項就是式(6),以後各項和κ有關。κ為三階相關係數,它也是未知量,因而方程不封閉。早期的均勻各向同性相關理論就是研究這一方程的各種封閉方法和解的形式。
對ui u' jˉ 進行傅立葉變換,得三維能譜函式:
式中k為波數。記E(k,t)=2πk2 Eij (k,t),它也是個三維能譜函式。同卡門-豪沃思方程相對應的能譜方程為:
式中F和三階速度相關函式有關。因而能譜方程也不封閉,它包含有兩個未知量E和F。
將能譜函式E對k積分就得湍能:
因此,E(k,t)dk就是那些波數處於k和dk之間的湍動渦的能量。如圖所示,在能譜曲線(E對k的曲線)中,小波數對應於大湍動渦,大波數對應於小湍動渦。對於中間尺度的渦,A.H.柯爾莫戈羅夫給出它的能譜是按k的-5/3次冪變化的,即在圖中的慣性子區,能譜曲線可表示為E=Aε
2/3 k
-5/3 ,式中ε為湍能耗散率。這一形式稱為柯爾莫戈羅夫譜定律。大量觀察到的數據支持這一定性結果。
能譜曲線示意圖 對各級湍渦的關係有一種級串觀點。湍流一旦形成,總的變化趨勢是大渦逐漸向中渦演變,中渦又向小渦演變。反映在能譜曲線的演變上,小k處的E值因大渦減弱而逐漸減小;中k處的E值一方面接受從較小k值區傳來的能量,一方面又向較大k值區輸送能量,最後因流體粘性的作用,能量在一些微小尺度的渦上轉化為熱而耗散掉。均勻各向同性湍流的譜理論就是從研究譜方程(8) 的封閉方法來導出能譜曲線的具體形式及其衰減規律的。
1941年,柯爾莫戈羅夫提出局部各向同性概念。他認為實際流動總有邊界的影響,因此受邊界影響較大的大尺度渦旋的運動不可能是各向同性的,而受邊界影響較少的小尺度渦旋則可能是各向同性的。為了消除大渦旋的影響,他研究了相對速度w
i =v
i -v
' i 和由此導出的結構函式,並認為由脈動場wi確定的平均性質具有各向同性,因此稱這種湍流為局部均勻各向同性湍流。周培源等從另一途徑,先解納維-斯托克斯方程,然後對所得的基元渦進行統計平均來研究均勻各向同性湍流,得出了相關量的衰減規律。此外,也有人開展了均勻剪下湍流的研究。R.H.克賴希南提出了直接相互作用理論;S.格羅斯曼把重正化群論方法引進湍流研究;S.楚格、M.B.劉易斯和B.B.斯特魯明斯基等開展了湍流的氣體動力論研究,但都未取得重要進展。
湍流經過一百多年的研究只得到極少量的定量預測。一、二十年來關於湍流結構的一些新發現,關於由不穩定、分岔而導致混沌的機械系統和數學系統的發現,有可能為理解湍流的發生提供新途徑。科學家和工程師們開始更多地考慮湍流機理。但是,這種對機理的思考不會很快地對完全發展的湍流作出徹底的了解,而只可能為構造更精確反映湍流過程基本機理的統計假設提供條件。
建立湍流理論是一個非常艱巨的任務。如今的任務是提高控制不穩定的技術和增強關於湍流
統計 模式的預測能力,由此推進工業新產品的設計,並且增強對天氣和海流等的預報能力。
參考書目







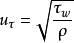











 能譜曲線示意圖
能譜曲線示意圖
