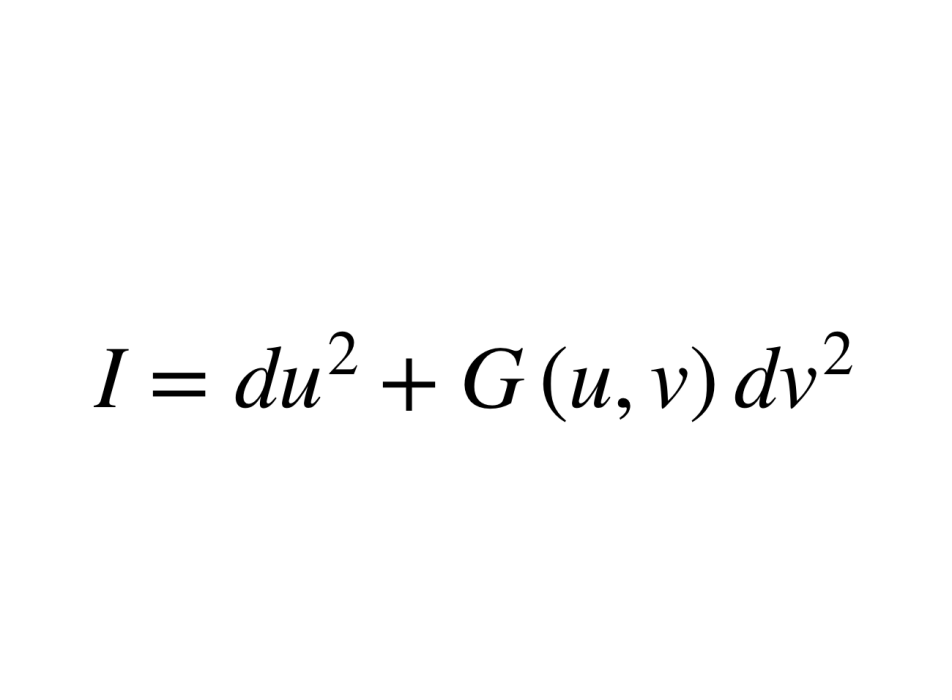測地坐標系

測地坐標系(geodesic coordinate system)曲面上的一種特殊坐標系。在曲面上取一族測地線為u曲線，取這族測地線的正交軌線為二曲線(稱為測地平行線)，這種坐標系稱為測地坐標系。

基本介紹

• 中文名：測地坐標系
• 外文名：geodesic coordinates
• 適用範圍：數理科學

簡介

測地坐標系是曲面上的一種特殊坐標系。在曲面上取一族測地線為u曲線，取這族測地線的正交軌線為二曲線(稱為測地平行線)，這種坐標系稱為測地坐標系。例，平面極坐標系，一族坐標曲線是由極點出發的射線，這是平面上的測地線，另一族坐標曲線是以極點為中心的同心圓，它們是上述測地線的正交軌線，因此平面極坐標系是一種測地坐標系。

測地坐標系分成測地平行坐標系和測地極坐標系兩種。測地坐標是在曲面內蘊幾何學意義下最簡單、最適當的坐標系。

建立方法

測地平行坐標構作如下：

取一條測地線C₀作為u=0曲線；經過曲線C₀上每一點、沿著C₀正交的方向作測地線，得到依賴一個參數的測地線族作為u曲線族；再作上述測地線族的正交軌線，作為v曲線族。此時，曲面的第一基本型成為

其中函式G（u，v）滿足條件

測地平行坐標系中曲線C0點附近是成立的。

測地極坐標系的構作如下：

取一點p，從點p出發沿各個切方向作測地射線，得到依賴一個參數的測地射線族，作為u曲線族；再作以點p為中心點測地圓（geodesic circle），即到點p的距離為常數的點點軌跡，作為v曲線族。此時，這兩族曲線是彼此正交的，故曲面的第一基本型成為

其中函式G（u，v）滿足條件

測地極坐標系在點p的附近、除去從點p出發點一條測地射線以外的區域上是成立的。

測地線

曲面上測地曲率恆為零的曲線稱為該曲面上的測地線，測地線所滿足的微分方程是

或者寫成一般的形式

式中，是曲面的克氏符號，（也記成）是測地線的參數方程。當曲面作保長變換時，測地線變成測地線。因此，測地線是屬於曲面的內蘊幾何概念。當曲面上取正交參數曲線網時，測地線的微分方程成為