浮點乘法器是現代微處理器的重要組成部件,由IEEE定義的IEEE 754浮點標準是目前廣泛被採用的一個標準。一般來說,浮點乘法包括符號位異或、指數相加和尾數相乘三部分。
基本介紹
- 中文名:浮點乘法器
- 外文名:floating-point multiplier
- 簡稱:FMULT
- 學科:計算機科學與技術
- 類別:乘法器
- 浮點標準:IEEE 754浮點標準
介紹
浮點標準


結構

實現



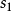










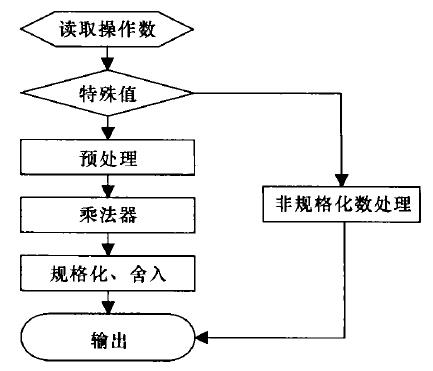

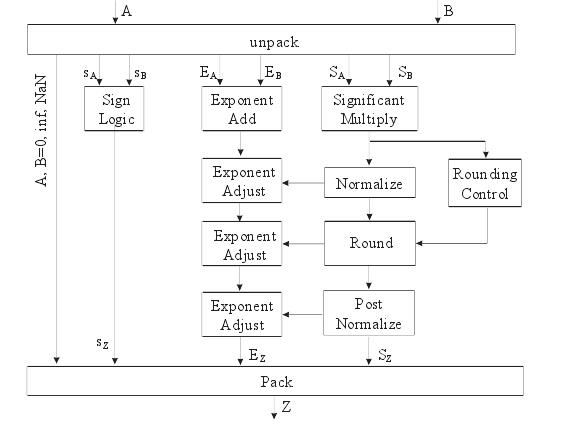
浮點乘法器是現代微處理器的重要組成部件,由IEEE定義的IEEE 754浮點標準是目前廣泛被採用的一個標準。一般來說,浮點乘法包括符號位異或、指數相加和尾數相乘三部分。






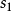












浮點乘法器是現代微處理器的重要組成部件,由IEEE定義的IEEE 754浮點標準是目前廣泛被採用的一個標準。一般來說,浮點乘法包括符號位異或、指數相加和尾數相乘三部分。...
每秒浮點運算次數(FLOP),按照IEEE 754標,FLOP被定義為單精度(32位)或者雙精度(64位)數加法或者乘法...
單功能流水線:只完成一種如乘法或浮點運算等,多用於數位訊號處理器(DSP),各處理器可並行完成各自的功能,加快整機處理速度。多功能流水線:在不同情況下可完成不同...
著的提升,使用了全新的浮點加法運算法則,大大降低了 x86處理器中的浮點延遲時間(the lowest floating-point add latency),同樣,浮點乘法器也擁有了最低的浮點延遲...
著的提升,使用了全新的浮點加法運算法則,大大降低了 x86處理器中的浮點延遲時間(the lowest floating-point add latency),同樣,浮點乘法器也擁有了最低的浮點延遲...
與此同時,Phenom還擁有兩個雙精度浮點乘法器和兩個雙精度浮點加法器以及三個數據搬移器,這也將確保其強悍的浮點性能。Phenom處理器採用了新一代超傳輸匯流排3.0,速度...
在這個晶片上,有兩個32位浮點乘法器。這個晶片作為多處理器晶片的演示晶片。PIM體系結構研究已經提出了滿足HTMT需求的PIM體系結構並進行了軟體模擬。其他項目對PIM...
它能提供友好的仿真環境,是業界唯一的單核心支持VHDL和Verilog混合仿真的仿真器。...實例4-2 32位浮點乘法器的Verilog仿真過程 984.3 SystemC仿真 104...
(5)“一種支持定浮點可重構的橫向求和網路結構”, 王東琳,閆寒,尹志剛,林嘯,謝少林,張志偉,薛曉軍(6)“支持複數運算和子字並行的64位定浮點乘法器”, 王東琳,...
著的提升,使用了全新的浮點加法運算法則,大大降低了 x86處理器中的浮點延遲時間(the lowest floating-point add latency),同樣,浮點乘法器也擁有了最低的浮點延遲...
著的提升,使用了全新的浮點加法運算法則,大大降低了 x86處理器中的浮點延遲時間(the lowest floating-point add latency),同樣,浮點乘法器也擁有了最低的浮點延遲...
它能提供友好的仿真環境,是業界唯一的單核心支持VHDL和Verilog混合仿真的仿真器。...實例4-2 32位浮點乘法器的Verilog仿真過程 984.3 SystemC仿真 104...
