基本介紹
- 中文名：洛希極限
- 外文名：Roche limit
- 所屬學科：天文學
- 提出者：愛德華·洛希
- 時間：1848年
名詞概觀,潮汐力,物理圖像,計算方法,潮汐力,計算洛希極限,公式修正,剛體洛希極限,流體洛希極限,其它結合力,套用舉例,軌道半徑與洛希極限比值,蘇梅克-列維九號彗星,
名詞概觀
潮汐力
任何一個有質量的天體總是會對其它天體施加萬有引力，而引力隨兩天體之間的距離增加而減小，因此站在受力天體的角度，位於其表面的單位質量與位於質心處的單位質量所受的引力會由於到引力源的距離不同而存在微小差別，我們將這個引力差稱為潮汐力。對於受力天體來說，潮汐力會沿該天體質心與施力天體連線方向拉伸該天體，且兩天體相距越近，潮汐力就越大，該天體就越容易被拉扯碎裂。
物理圖像
潮汐力會隨著兩個天體的距離減小而增加，所以在兩個天體逐漸靠近的過程中，如果它們的密度足夠大，而且為兩個天體相互接近留下了足夠的空間，那么就會存在一個極限距離，在該距離之內，其中一個較小天體恰好因為潮汐力而開始瓦解。在最初計算這個極限距離時，為了使模型更加簡潔，不妨假設即將碎裂的天體僅依靠引力結合在一起（事實上像地球這種固態行星作為一個整體，它的組成物質相互之間還會有應力將彼此連線在一起），此外我們還假設在解體前，該天體形狀保持一個完美的球形，那么顯然，當該天體表面物質受自身的引力小於潮汐力時，其表面物質就會脫離，因此，洛希極限就是計算潮汐力等於自身引力時的距離，我們把以該種方法計算的極限距離稱為洛希極限。但實際中，天體不一定僅由引力結合在一起，也不可能是一個完美的球體，所以天體解體的距離並不嚴格等於使用剛才方法所計算的洛希極限，因此需要對模型進行修正。
計算方法
潮汐力
因為洛希極限定義為受力天體恰好開始瓦解的距離，也就是只需要根據受力天體所受潮汐力豎直分量最大的一點處是否開始瓦解即可判斷洛希極限的位置，所以此處就不給出潮汐力完整的證明，只計算潮汐力最大一點處的潮汐力。而這個潮汐力豎直分量最大的點就位於受力天體距施力天體的最近處。
設施力天體質量為M、施力天體與受力天體質心距離為d、受力天體半徑為r。
根據牛頓萬有引力定律，受力天體質心加速度大小為
。而距施力天體最近處的加速度大小為
，則根據定義，潮汐力對應的加速度為
。使用泰勒展開，可將展開為
，在討論中可以認為r<<d，因此將
的高階項近似為零，可得潮汐力為
。
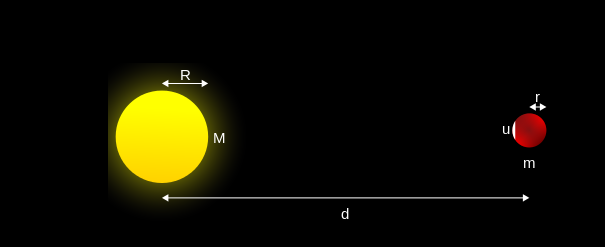
計算中使用的物理量
計算洛希極限
假設受力天體僅依靠自身引力維持形態、受力天體的形狀是完美的球形，且在到達洛希極限前不因潮汐力而變形。
考慮受力天體表面最接近施力天體處的部分質量為μ，有兩股力作用在μ上：受力天體自身對它的引力和施力天體對它產生的潮汐力。
設FG為受力天體作用在μ上的引力，根據牛頓引力定律，
。
設d.為受力天體與施力天體中心的距離，r為受力天體半徑，FT為施力天體作用在μ上的潮汐力，
若受力天體剛好位於洛希極限處，則有FG=FT，即
由此即可計算出
一般我們不希望受力天體的半徑出現在公式中，因為洛希極限實際上是由天體密度等更基礎的性質決定的，因此將公式中的半徑以密度等量寫出。
施力天體的質量可寫成：
受力天體的質量可寫成：
代入上面的洛希極限的公式，得
簡化成：
公式修正
剛體洛希極限
上文所計算的洛希極限實質上就是剛體洛希極限，它是默認受力天體不會形變且僅由引力結合這兩個近似下的物理模型。這種模型很適合討論例如碎石堆小天體、彗星等天體，對於類似於地球這樣的天體可以近似討論，但由於地球組成物質之間彼此綁定的應力，單純剛體洛希極限的計算結果會與地球這種相對彗星大很多的行星的實際情況有所差異。
流體洛希極限
流體洛希極限與剛體洛希極限相對，在這個模型下我們假設受力天體是完美的流體，因此即使天體間距超過洛希極限，潮汐力會將受力天體拉長，從而導致潮汐力增加，進而導致其更容易碎裂。洛希所給出的公式為：
更精確的公式為：
可見它的係數比剛體洛希極限的大。
現實中，大部分天體都介於完美剛體與完美流體之間，因此它們真實的洛希極限介於剛體與流體洛希極限之間。
其它結合力
所以在討論一些如人造衛星等物體時，通過使引力等於潮汐力計算出來的洛希極限完全不適用了，衛星內部的結合作用遠遠大於引力。
套用舉例
軌道半徑與洛希極限比值
下表展示了太陽系內天體所處的軌道與洛希極限之比，可以看出很多衛星處於剛體洛希極限與流體洛希極限之間，而很少有天體位於剛體洛希極限之內。
施力天體 | 受力天體 | 軌道半徑:洛希極限 | |
剛體 | 流體 | ||
太陽 | 水星 | 104:1 | 54:1 |
地球 | 月球 | 41:1 | 21:1 |
火星 | 火衛一 | 1.72:1 | 0.89:1 |
火衛二 | 4.51:1 | 2.33:1 | |
木星 | 木衛十六 | 1.86:1 | 0.93:1 |
木衛十五 | 2.2:1 | 1.1:1 | |
木衛五 | 2.28:1 | 1.14:1 | |
木衛十四 | 2.6:1 | 1.29:1 | |
土星 | 土衛十八 | 1.74:1 | 0.85:1 |
土衛十五 | 1.82:1 | 0.89:1 | |
土衛十六 | 1.85:1 | 0.9:1 | |
土衛十七 | 1.85:1 | 0.9:1 | |
土衛十一 | 1.98:1 | 0.97:1 | |
天王星 | 天衛六 | 1.55:1 | 0.79:1 |
天衛七 | 1.67:1 | 0.86:1 | |
天衛八 | 1.84:1 | 0.94:1 | |
天衛九 | 1.92:1 | 0.99:1 | |
海王星 | 海衛三 | 1.4:1 | 0.72:1 |
海衛四 | 1.49:1 | 0.77:1 | |
海衛五 | 1.53:1 | 0.78:1 | |
海衛六 | 1.84:1 | 0.95:1 | |
海衛七 | 2.2:1 | 1.13:1 | |
蘇梅克-列維九號彗星
蘇梅克-列維九號彗星是一顆太陽系內的彗星，它在1994年7月17日4時15分與木星撞擊，為科學家對木星的研究提供了很大的幫助。
有趣的是，這顆彗星並未直接撞擊木星，而是在距離木星表面約四萬公里時分解成了21個碎塊，這正是因為彗星達到了它在木星周圍的剛體洛希極限。
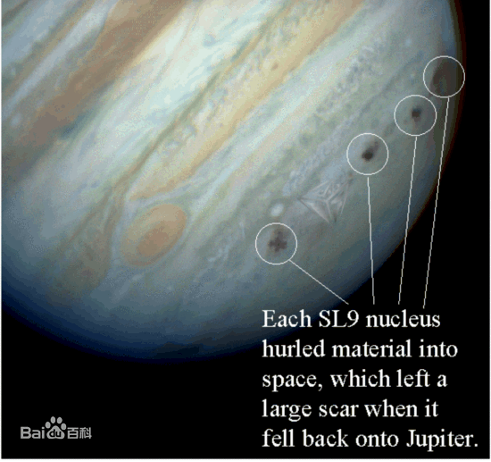
彗星解體後撞擊木星留的痕跡
