基本介紹
- 中文名:洛希極限
- 外文名:Roche limit
- 提出者:愛德華·洛希
- 時間:1860年
- 學科:天文學
- 套用:衛星
簡介,計算方法,公式導出,流體的洛希極限公式,套用,例子,
簡介
洛希極限(Roche limit)是一個天體自身的引力與第二個天體造成的潮汐力相等時的距離。當兩個天體的距離少於洛希極限,天體就會傾向碎散,繼而成為第二個天體的環。它以首位計算這個極限的人愛德華·洛希命名。
洛希極限常用於行星和環繞它的衛星。有些天然和人工的衛星,儘管它們在它們所環繞的星體的洛希極限內,卻不至成碎片,因為它們除了引力外,還受到其他的力。木衛十六和土衛十八是其中的例子,它們和所環繞的星體的距離少於流體洛希極限。它們仍未成為碎片是因為有彈性,加上它們並非完全流體。在這個情況,在衛星表面的物件有可能被潮汐力扯離衛星,要視乎物件在衛星表面哪部分——潮汐力在兩個天體中心之間的直線最強。一些內部引力較弱的物體,例如彗星,可能在經過洛希極限內時化成碎片。蘇梅克-列維9號彗星就是好例子。它在1992年經過木星時分成碎片,1994年落在木星上。現時所知的行星環都在洛希極限之內。
計算方法
設洛希極限為d。

對於一個完全剛體、圓球形的衛星,假設其物質都是因為重力才合在一起的,且所環繞的行星亦是圓球形,並忽略其他因素如潮汐變形及自轉。

其中R是衛星所環繞的星體的半徑,ρM是該星體的密度,ρm是衛星的密度。
對於是流體的衛星,潮汐力會拉長它,令它變得更易碎裂。

由於有黏度、摩擦力、化學鏈等影響,大部分衛星都不是完全流體或剛體,其洛希極限都在這兩個界限之間。如果一個剛體衛星的密度是所環繞的星體的密度兩倍以上(例如一個巨大的氣體行星跟剛體衛星;對於流體衛星來說,則要約14.2倍以上),d<R,洛希極限會在所環繞的星體之內,即是說這個衛星永遠都不會因為所環繞的星體的引力而碎裂。
公式導出
假設除了引力之外沒有其他力,且衛星和所環繞的行星的形狀是圓球。
考慮衛星表面的最接近行星的細質量 μ,有兩股力作用在 μ上:衛星的引力和行星的引力。基於衛星在行星引力場內自由降落,潮汐力不過是行星引力同義詞。
設  為衛星作用在 μ上的引力,根據牛頓引力定律,
為衛星作用在 μ上的引力,根據牛頓引力定律, 。
。


設d為衛星和行星中心的距離,R為行星半徑, 為行星作用在 μ上的潮汐力,
為行星作用在 μ上的潮汐力,


若衛星剛好在洛希極限,  ,即
,即


由此即可計出
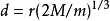
不想衛星半徑出現在公式中,便將其半徑以密度等變數寫出。
行星的質量可寫成:

衛星的質量可寫成:

代入上面的洛希極限的公式,得
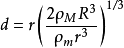
簡化成:
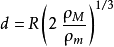
流體的洛希極限公式
洛希給出的基於流體洛希極限的公式是:

更精確的公式是:

c/R是行星的扁度。
公式的推導過程較複雜,此處不予給出。
套用
最常套用的地方就是衛星和它所環繞的星體。有些天然和人工的衛星,儘管它們在它們所環繞的星體的洛希極限內,卻不至成碎片,因為它們除了引力外,還有其他的力幫助。在這些情況下,在衛星表面的物件有可能被潮汐力扯離衛星,要視乎物件在衛星表面哪部分——潮汐力在兩個天體中心之間的直線最強。
一些內部引力較弱的物體,例如彗星,可能在經過洛希極限內時化成碎片。蘇梅克-列維9號彗星就是好例子。它在1992年經過木星時分成碎片,1994年落在木星上。現時所知的行星環都在洛希極限之內。
例子
以太陽系內的星體為例:
使用以上數據,計算流體及剛體洛希極限。R表示它們和真正的洛希極限之比。
天體 | 衛星 | 剛體洛希極限距離(m) | 剛體洛希極限R | 流體洛希極限距離(m) | 流體洛希極限R |
地球 | 月球 | 9,495,665 | 1.49 | 18,261,459 | 2.86 |
17,883,432 | 2.80 | 34,392,279 | 5.39 | ||
太陽 | 地球 | 554,441,389 | 0.80 | 1,066,266,402 | 1.53 |
木星 | 890,745,427 | 1.28 | 1,713,024,931 | 2.46 | |
月球 | 655,322,872 | 0.94 | 1,260,275,253 | 1.81 | |
彗星 | 1,234,186,562 | 1.78 | 2,373,509,071 | 3.42 |
對比驗算
主星 | 附屬星 | 質量(kg) | 半徑 (km) | 原洛希極限公式 d=R×(2×ρM/ρm) | 建議修改公式 d=r×(3×M/m) | ||||
洛希極限 | 希爾球半徑 | 結果 | 洛希極限 | 希爾球半徑 | 結果 | ||||
地球 | 月球 | 7.35E+19 | 1737.4 | 94831.1 | 1517.7587 | 已解體 | 108555 | 1737.4 | 解體極限 |
彗星 | 1.67552E+13 | 2 | 17870.1 | 1.7471609 | 已解體 | 20456.2 | 2 | 解體極限 | |
太陽 | 地球 | 5.98E+24 | 6371 | 556279 | 5565.5811 | 已解體 | 636780 | 6371 | 解體極限 |
木星 | 1.90E+27 | 71500 | 914695 | 62461.003 | 已解體 | 1047065 | 71500 | 解體極限 | |
月球 | 7.35E+19 | 1737.4 | 6571920 | 1517.7587 | 已解體 | 7522971 | 1737.4 | 解體極限 | |
彗星 | 1.67552E+13 | 3 | 1857633 | 2.6207414 | 已解體 | 2126459 | 3 | 解體極限 | |
衛星處於原洛希極限公式所得位置時基本上完全解體;
按修改建議的洛希極限公式,衛星處於該位置時,希爾球剛好在星衛星表面,正是解體的臨界點。
後文中的“太陽系的行星和其衛星之間的真實洛希極限”,有興趣的朋友可以自行驗算對比一下。
太陽系的行星和其衛星之間的真實洛希極限和計算洛希極限如下表所示:
天體 | 衛星 | 軌道半徑:洛希極限 | revise | ||
剛體 | 流體 | 用(3)式驗算 | 用(2)式驗算 | ||
太陽 | 104:1 | 54:1 | 640554442 | 640563260 | |
地球 | 月球 | 41:1 | 21:1 | 10861728 | 10860447 end revise. |
火星 | 172% | 89% | |||
451% | 233% | ||||
木星 | 186% | 93% | |||
220% | 110% | ||||
228% | 114% | ||||
260% | 129% | ||||
174% | 85% | ||||
182% | 89% | ||||
185% | 90% | ||||
185% | 90% | ||||
198% | 97% | ||||
155% | 79% | ||||
167% | 86% | ||||
184% | 94% | ||||
192% | 99% | ||||
140% | 72% | ||||
149% | 77% | ||||
153% | 78% | ||||
184% | 95% | ||||
220% | 113% | ||||

