泰博定理有三個,是由法國數學家維克多泰博根據不同情形的幾何問題提出來的,分別被稱為泰博定理I, II, III。
基本介紹
- 中文名:泰博定理
- 外文名:Thébault's theorem
- 提出者:Victor Thébault(維克多泰博)
- 套用學科:數學
- 適用領域範圍:幾何學
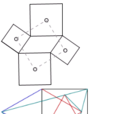
泰博定理I:取平行四邊形的邊為正方形的邊,作四個正方形(同時在平行四邊形內或外皆可)。正方形的中心點所組成的四邊形為正方形(此為凡·奧貝爾定理的特例)。
泰博定理II:給定一個正方形,在正方形兩條相鄰邊的內外構建兩組等邊三角形。然後,將遠離兩個三角形的正方形的頂點以及兩個遠離正方形的三角形的頂點連線起來,所構成的三角形是等邊的。
泰博定理III:給定任意的三角形ABC以及BC上任意一點M,構建三角形ABC的內切圓和外接圓。然後構造另外兩個圓,使得與AM,BC和(三角形ABC的)外接圓都相切。因此,這兩個圓的圓心和(三角形ABC的)內切圓的圓心共線。
直到2003年,學術界認為泰博第三定理是最難證明的。此定理由荷蘭數學家H. Streefkerk於1973年所證明並於1938年發表在美國數學月刊。但在2003年,Jean-Louis Ayme發現Y. Sawayama,一個在東京中央軍事學校的輔導員,獨立提出並在1905年解決了這個問題。