約翰·法雷 是英國一位多才多藝的“雜家”, 生活在拿破崙時代，職業是土地丈量員, 卻有著廣泛的愛好, 喜歡蒐集奇異的石頭、礦物, 興致來潮, 撰寫小塊科普文章在《哲學雜誌》上發表, 題材廣泛，涉及到地質、音樂、錢幣、車輪、慧星, 偶爾也涉及數學小品。1816年, 當他審讀亨利·戈德溫所編的“小數商表” 時,忽然有一個問題湧上心頭：既約最簡真分數有多少呢，能不能把它們按一定的順序排列出來？興致所及，急切難忍，他立即推開戈氏冗繁的“商表”，動手排列起來, 一遍又一遍, 沒有頭緒。這時他想到兩點：一是真分數有無限多個, 要“全部”排出, 必須限制分母的大小；二是可按遞增的順序去排列, 容易發現規律。他終於排出來了, 還發現了若干性質。發表後, 立即被當時數學家們抓住, 後來數學家柯西發現這分數串在數學中很有用,併名之為法雷數列。沒成想早在14年前, 一位名叫哈羅斯的人, 就發現並公布了自己的研究結果，故名之哈羅斯一法雷數列。
基本介紹
- 中文名：哈羅斯一法雷數列
- 外文名：Farey series
- 別名：法雷序列、法雷數列
- 提出者：法雷
定義,性質,例程,pascal碼,C++碼,
定義
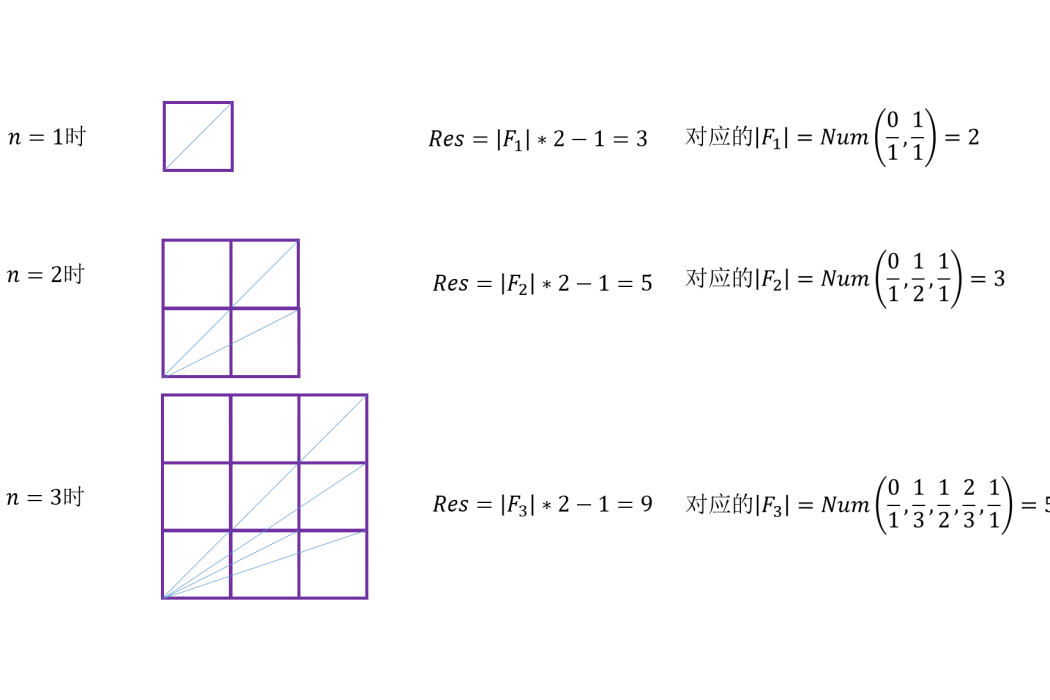
對任意給定的一個自然數n，將分母小於等於n的不可約的真分數按升序排列，並且在第一個分數之前加上0/1，在最後一個分數之後加上1/1，這個序列稱為n級法雷數列，以Fn表示。如F5為：0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1。
性質
- 除了1級法雷數列外，所有的法雷數列都有奇數個元素，其中居於正中間的那個元素一定是1/2.
- 當n趨於正無窮時，n級法雷數列包含的元素的個數趨於3/(π*π) * n2 ≈ 0.30396355 * n2.
- n級法雷數列中，若相鄰兩個元素是a/b 和c/d (a/b＜c/d),則這兩個數的差為1/bd, 這個差的最小值為1/(n*(n-1)), 最大值為1/n, 在法雷數列的第一個元素（0/1）與其後繼以及最後一個元素（1/1）與前驅之間的差取到最大值，而正中間的那個元素1/2 與其前驅和後繼元素之間的差取次大值1/(n*2).
- 在法雷數列中，對於任意兩個相鄰分數，先算出前者的分母乘以後者的分子，再算出前者的分子乘以後者的分母，則這兩個乘積一定剛好相差1.
實數化分數方法
對於有理數0，我們可以用0/1表示；對於有理數x＜0, 總可以表示為–(p/q), 其中p＞0,q＞0；而對於所有大於等於1的正有理數，總可以表示為n + p/q ( n, p, q為非負整數，q!=1, p＜q)的形式, 以分數形式可表示為(nq + p) /q。因此，轉化小於1的正有理數為分數是實數轉化為分數的基本問題。由於無理數不能用一個分數來準確的表示，因此，我們可用兩個分數a/b, c/d 來逼近這個實數，使得無理數f ＞= a/b且f＜=c/d，a/b稱為實數f的下界，c/d稱為實數f的上界，求這個下界和上界實際上是找出一個n級法雷數列中兩個相鄰的元素。下面是化一個小於1的正實數為分數的算法。
Step1: 置實數f 的下界為a/b=0/1, 上界為c/d =1/1。
Step2: 計算出下界和上界之間的數p/q = (a+c)/(b+d)
Step3: 若q＞n（分母大於指定值），計算中止。
若p/q =f，a/b ßp/q , c/d ßp/q, 計算中止。
若p/q ＞ f, 置下界a/b為p/q
若p/q＜ f, 置上界c/d為p/q
Step4, 重複step 2-3
當計算終止時，a/b為這個實數的下界，c/d為這個實數的上界。
如果要轉化的實數f小於1/2, 用上述逐步求精的步驟，計算出上下界，疊代次數稍多。我們可用下面的步驟代替step1, 直接找出一個更精確的上下界。
若e= 1/x 的向下取整，則這個實數的下界和上界為1/(e+1)和1/e
誤差分析，根據法雷數列性質3我們知道，n級法雷數列中相鄰的兩個元素可以表示一個區間[a/b, c/d]，前一個元素a/b為區間的下界，後一個元素c/d為區間的上界，這個區間的寬度h =c/d- a/b,滿足1/(n*(n-1)) ＜= h ＜=1/n。若運氣好的話，一個實數正好落在一個寬度為1/n(n-1) 的區間，這個區間的下界或上界與這個實數的差不超過abs(1/(n*(n-1)))。若運氣很差，一個實數恰好小於法雷序列的第2個元素或者最後一個元素。則這個元素的下界和上界與這個實數的差不超過1/n。
例程
pascal碼
{
PROG: frac1
LANG: PASCAL
}
program frac1;
type node=record
x,y:longint;
d:double;
end;
var n,i,j,len:longint;
sn:array[1..8000]of node;
function gcd(x,y:longint):longint;
begin
if x=0 then gcd:=y
else gcd:=gcd(y mod x,x);
end;
procedure qsort(s,t:longint);
var i,j:longint;
mid:double;
te:node;
begin
i:=s;j:=t;mid:=sn[(s+t)div 2].d;
while i＜=j do
begin
while sn[i].d＜mid do inc(i);
while sn[j].d＞mid do dec(j);
if i＜=j then
begin
te:=sn[i];sn[i]:=sn[j];sn[j]:=te;
inc(i);dec(j);
end;
end;
if i＜t then qsort(i,t);
if s＜j then qsort(s,j);
end;
begin
// while not eof do begin
read(n);
sn[1].x:=0;sn[1].y:=1;sn[1].d:=0.0;
sn[2].x:=1;sn[2].y:=1;sn[2].d:=1.0;
len:=2;
for i:=2 to n do
for j:=1 to i-1 do
if gcd(i,j)=1 then //判斷是否是真約數
begin
inc(len);
sn[len].x:=j;sn[len].y:=i;sn[len].d:=j/i;
end;
qsort(1,len);
for i:=1 to len do
writeln(sn[i].x,'/',sn[i].y);
//end;
close(input);close(output);
end.
C++碼
#include＜cstdio＞
using namespace std;
long n;
void dfs(long x1,long y1,long x2,long y2){
if(y1+y2＜=n){
dfs(x1,y1,x1+x2,y1+y2);
printf("%d/%d\n",x1+x2,y1+y2);
dfs(x1+x2,y1+y2,x2,y2);
}
}
int main()
{
scanf("%d",&n);
printf("0/1\n");
dfs(0,1,1,1);
printf("1/1\n");
return 0;
}
