決策關鍵線路法

決策關鍵線路法 (DCPM ) 是在傳統的網路計畫(CPM/PERT ) 基礎上發展起來的一種網路技術， 它將方案決策和工程進度安排這兩項工作同時進行，從而得到工程總體最優的網路計畫。

基本介紹

• 中文名：決策關鍵線路法
• 外文名：Decision Critical Path Method;
• 英文縮寫：DCPM
• 同類：CPM/PERT
• 套用：網路計畫
• 領域：計算機網路

規定簡介

關鍵路線法和計畫評審技術已為各行各業各部門廣泛採用，成為計畫管理的有力工具。但是這些方法主要著 眼於時間，總是從工期上進行分析和計算，儘量做到按規定工期或在儘可能短的時間內完成。在網路圖中沒有反 映資源（人力、物力）和成本，而這些卻又是工程規劃中必須考慮的，這就需要進一步研究時間——資源和時間——成本問題。

每項活動需要多種資源，它們之間存在一種最優配置，那么各種資源的消耗也可以用成本來反映。考慮到有些活動由於採用了不同的技術、不同的資源（也可以是同種資源數量上的增減）或不同的組織方式，需要的成本不同，完成的工期也不同，這就產生了不同的方案。有時為了縮短某項活動的工期動用了某種緊張的資源或增加 了某種緊張資源的數量，我們也可以大大提高該資源消耗所反映的那部分成本，從而間接地反映出資源的約因此 ，我們著重分析時間成本問題。

在上面所講到的不同方案中，我們總是希望選擇在下面兩種意義中的一種最優方案工期一定而成本最低；成本一定而工期最短。為了解決這一問題，近年來發展了考慮成本與工期關係的網路計畫法，先找到成本與工期的近似函式關係，然後用數學規劃的思想和方法找出最優解。這種方法由於成本與工期的函式關係較難獲得而沒有得到很大的推廣。

在工程實踐中，某些活動可供選擇的方案成本與工期不同數目常常是有限的，而需要作出決策的場合也是有限的。不需要處理複雜的函式關係。

舉例來說，在製造混凝土預製件時，對澆灌後的構件在拆模前可以澆水養生，經過較長時間後方能拆模。在澆灌後也可以採用蒸汽養生的方法，迅速提高早期強度，拆模。因此拆模前的養生採用澆水和蒸汽養生兩種，前者的時間長成本低，後者卻相反。再如，需要某設備或部件，可以採用本單位加工和外協的方法。在本單位加工 雖然成本較低，但在能力有限或加工任務趨於飽和時加工周期長。如委託外單位加工，時間雖短但成本較高。以上兩個例子都說明，在某一項活動中，只有有限個兩、三個或再多一點可供選擇的方案，而且在整個工程中，也只有為數不多的幾個活動有這種選擇餘地。

在編制網路圖時怎樣反映這種可供選擇的情況呢？一種方法是針對每種情況畫一張網路圖，作為一種方案，然後進行分析比較，這樣做不勝其繁。另一種方法就是近年來有人提出的決策關鍵線路法(簡稱DCPM) ,這種方法的特點是在一般的網路圖(採用單代號網路圖)上增加一些決策點,表明在這些活動上有不同的方案可供選擇。一個 網路圖可以有多個決策點，反映出有多個需要作出選擇的活動。每個決策點上有幾個可供選擇的方案（每個方案 工期、成本都不同），由擬訂計畫的人全面地根據工期、成本加以分析，選擇合理的實施方案。

DCPM除了能在任務開始前進行決策外，也可以在執行過程中採用。由於某種原因，有幾項活動耽誤了時間，影響了整個工期。此時開始認為合理的方案就不一定是合理的了。因此在可能的情況下，可以根據此刻的條件重新進行決策，來選擇新情況下的合理方案。

因此，DCPM與CPM相比，它可以提供多種可能來供領導進行決策時使用，不象CPM只是一種可能。

DCPM比較適合於我們在工作中進行比較決策用，特別適合供領導進行決策和使用。

DCPM的表示法

令任務

為1到n項活動之集合，活動Si在單代號網路圖中可以用節點O表示。活動間的邏輯關係可以用節點間的帶箭線段表示。

這樣，網路圖就是集合J和在J上定義的先行關係。

在DCPM中，除了那些必須完成的活動外，某些活動是若干項互斥活動的集合。這些活動可以表示為

這些互斥活動中有一項完成了就標誌著該決策活動的完成。在單代號網路圖中用圖1表示。同樣可

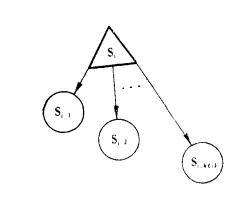
圖1

以用帶箭頭的線段表示活動間的關係。我們採用決策變數 來表示活動 的完成與否。若活動 必須完成，則 為1，若活動 不去完成，則 為0。

因此，DCPM的網路圖就是集合J和J上定義的先行關係及決策活動上定義的互斥關係。

在DCPM的網路圖中由於決策活動中活動 的互斥性，其中一些活動是 要完成的，而另一些活動就不必完成。這些不完成的活動在網路圖中將消失，與這些活動有關的緊前、緊後關係也將隨之消失，為了保證網路圖中先行系統的正確性，我們必須考慮到：（1）如果 只有唯一的緊前活動 ,就必須在 的緊前活動中增加一個 的緊前活動。這樣可以避免一旦 消 失後， 失去唯一的緊前活動。（2）同樣當 有唯一的緊後活動 , 也必須在 的緊後活動中增加一個 的緊後活動。（3）如果兩個活動是由 連結起來的，雖然它們具有多個緊前活動和緊後活動，為了在 消失的情況下仍能保持兩者間的邏輯關係，也需增加一個關係。 三種情況的網路圖如圖2中的a，b，c。

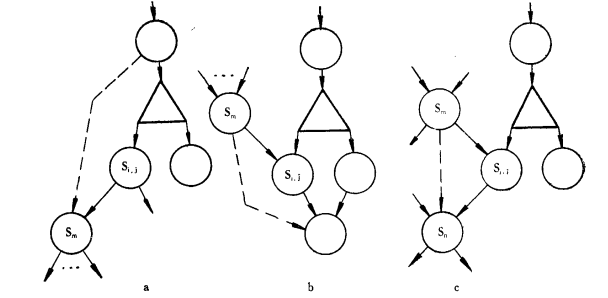
圖2

DCPM的改進算法

原網路圖是用單代號表示，但是我國廣大工程技術人員所熟悉的CPM和PERT網路圖大都是雙代號表示的，DCPM與CPM及PERT存在著密切的聯繫，為了便於套用，我們把單代號DCPM網路圖改用雙代號表示。

雙代號DCPM網路圖採用了雙代號CPM及PERT的網路結構，並在此基礎上增加決策工序，其表示形式見圖3。這裡，I表示以決策點為始點的決策工序；表示決策工序（I,J）的第i個選擇第j個方案,決策工序中的虛箭線只起邏輯聯繫作用，沒有其它含意。

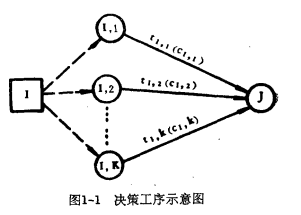
圖3

圖4為一個具有4個決策工序和5個非決策工序的雙代號網路圖。

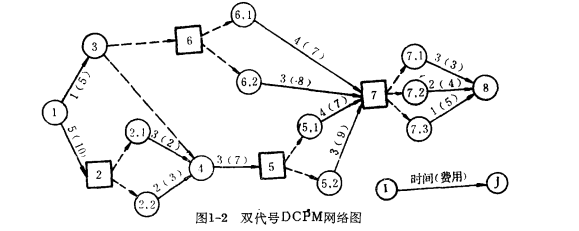
圖4

在雙代號網路圖中，一個決策點只能表示一個，且僅僅一個決策工序的開始，不能有兩個或多個工序的始點為同一決策點，但是可以有兩個或多個工序的終點為同一決策點，在雙代號網路圖中允許有虛工序存在，應注意和決策工序中的虛箭線的區別。