決策樹歸納法(DTI),又稱“決策圖”,是歸納式學習法中最簡單的一支。它是將決策過程各個階段之間的邏輯結構繪成一張箭線圖,再根據決策樹進行分析計算,從而得出所需決策方案的方法。DTI常用於數據挖掘。
基本介紹
- 中文名:決策樹歸納法
- 外文名:Decision Tree Induction
- 別稱:決策圖
- 簡稱:DTI
- 套用:數據挖掘
- 相關概念:決策樹
簡介,DTI算法原理,DTI算法步驟,算法偽程式示例,示例偽程式解釋,
簡介
決策樹歸納法根據數據的值,把數據分層組織成樹型結構,即用樹形結構來表示決策集合,這些決策集合通過對數據集的分類產生規則。在決策樹中每一個分支代表一個子類,樹的每一層代表一個概念。
決策樹歸納法一般以方框和圓圈為結點,並由直線連線而成的一種像樹枝形狀的結構。方框結點叫做決策點,由決策點引出若干條樹枝(直線)。每條樹枝代表一個方案,故叫方案枝。在每個方案枝的末端畫上一個圓圈就是圓圈結點,圓圈結點叫做機會點。由機會點引出若干條樹枝(直線),每條樹枝為機率枝。在機率枝的末端列出不同狀態下的收益值或損失值。
DTI常用於分析構建模型的可行性與可信度,相應地根據觀察推出其邏輯表達式及結構,通過其簡單清晰的邏輯推理和分割信息值,能夠快捷地對大數據集進行高效的數據劃分。但針對連續型數據和多類別集合,劃分效率就會隨複雜度的升高而降低。
DTI算法原理
決策樹歸納法( GTI) 是一組規則集合,使用遞歸的方式將訓練樣本集( TS) 劃分成更小的子集合(Sub-TS) ,直到每一個子集合擁有獨有的所屬類別標籤。
DTI算法通常採用資訊理論(IT)作為屬性選擇方法,根節點TS的選擇是基於訓一算出的所具有最高信息增益的屬性。給定一個N維訓練樣本集T={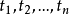 },
},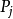 表示樣本實例
表示樣本實例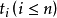 屬於類別
屬於類別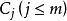 的先驗機率,可根據下式得出對給定的樣本實例進行分類所需要的期望信息Info(T)。
的先驗機率,可根據下式得出對給定的樣本實例進行分類所需要的期望信息Info(T)。
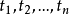
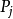
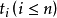
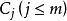
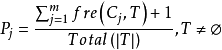

相應地,訓練樣本集T根據屬性A={ }疊代地被劃分成N個不同的子集合{
}疊代地被劃分成N個不同的子集合{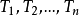 },其中
},其中 為樣本集合T中屬性A=
為樣本集合T中屬性A= 時的樣本子集合。可根據權重值
時的樣本子集合。可根據權重值 計算出屬性A劃分T的期望信息,從而根據原始信息要求Info (T)和新的信息要求的偏移量計算得出信息增益InfoGain(A)。根據樣本集T中的屬性值,逐一地計算出每個屬勝值對T進行劃分的信息增益,從中選擇出具有最高信息增益的屬性
計算出屬性A劃分T的期望信息,從而根據原始信息要求Info (T)和新的信息要求的偏移量計算得出信息增益InfoGain(A)。根據樣本集T中的屬性值,逐一地計算出每個屬勝值對T進行劃分的信息增益,從中選擇出具有最高信息增益的屬性 。作為最佳屬性來劃分子集合,遞歸整個過程直到所有集合都被正確歸類。
。作為最佳屬性來劃分子集合,遞歸整個過程直到所有集合都被正確歸類。

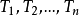




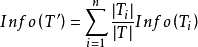
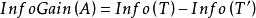
DTI算法步驟
算法偽程式示例
程式名:DTI
samples代表以離散值屬性表示的訓練樣本,attribute_list指候選屬性集合。
(1) 建立一節點N;
(2) 若samples含相同分類c,則:
(3) 返回N表示含c類的葉節點;
(4) 若attribute_list為空集合則:
(5) 返回N含samples中最大類的葉節點;
(6) 選test_ attribute,即attribute_ list中含最大信息增益的屬性;
(7) 將節點N標記為test attribute;
(8) 對test attribute的每一已知值 分割樣本;
分割樣本;

(9) 由節點N產生一分支表示test attribute=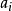 ;
;
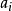
(10) 令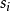 為samples中test_attribute=
為samples中test_attribute=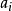 的樣本集合;
的樣本集合;
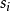
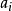
(11) 若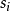 為空集合,則:
為空集合,則:
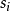
(12) 新增一葉節點且標記以samples中最大類;
(13) 否則新增一節點(由DTI(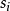 ,attribute_ list,test_attribute)產生)。
,attribute_ list,test_attribute)產生)。
示例偽程式解釋
樹由一單一節點表示訓練樣本開始(步驟 1),若樣本含相同類,則節點為葉且註標為此類(步驟 2、 3); 否則,算法使用系統亂度導向稱為信息增益法為經驗法則,以選出最能將樣本分成兩類的屬性(步驟 6)。該屬性變成該節點的“測試”或“決策”屬性(步驟 7)。算法的各屬性均被分類, 每一測試屬性的已知值建立一分支,樣本依此被分割(步驟 8-10)。 算法以遞歸式形成樣本中每一分割而成決策樹。節點產生一屬性後,則不需考慮該節點的子孫(步驟 13)。當滿足下列條件時停止遞歸:
(a) 樣本的任一已知節點皆屬於某一固定類(步驟 2、3)或
(b) 樣本中沒有其它屬性可供進一步分割(步驟 4),此時,引用勝者攘括(步驟 5),將該節點轉換成葉節點且標記為勝者的類別,否則儲存該節點的類分布。
(c) 分支 test_attribute=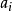 (步驟 11)無樣本。此時,葉依據樣本中主要類別建立(步驟 12)。
(步驟 11)無樣本。此時,葉依據樣本中主要類別建立(步驟 12)。
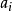
樹中每一節點所選的測試屬性均以信息增益加以衡量,這種衡量稱為屬性選擇度量或度量一完善的分割。含最高信息增益的屬性(或最大量的減少)被選為該節點的測試屬性。該屬性能將樣本分類所需信息最小化,且使分類所含雜質最小化。這種資訊理論方法使分割對象所需測試最小化且保證能得到一簡化樹。

