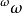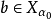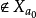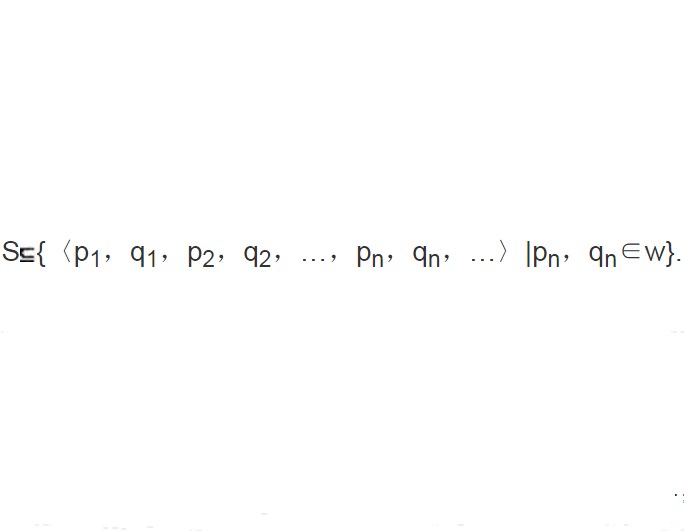決定性公理(determinstic axiom)是集合論的一條重要公理,在現代描述集合論中無窮對策具有重要的作用。考慮二人對策:設M={0,1,…,m-1},參賽者Ⅰ和Ⅱ輪流在M中選取n個數,得到結果序列,設為〈p1,q1,p2,q2,…,pn,qn〉,稱為一個結局。一個結局的集合S被事先給出並且為Ⅰ和Ⅱ知道.最後,若〈p1,p2,…,qn〉∈S,則Ⅰ獲勝;否則〈p1,p2,…,qn〉∉ S,則Ⅱ獲勝,把這種對策記為GS,許多二人參賽的智力遊戲,如下棋,都能在適當地選擇M,n和S後,以這一抽象的形式被數學地表示,Ⅰ的一種必勝策略是指一規則:在Ⅰ的每一步,該規則可以根據雙方在此以前的取法告訴Ⅰ這一步該怎樣取,最終使Ⅰ獲勝,類似地,可定義Ⅱ的必勝策略,在n是有窮的情況下,容易證明Ⅰ或Ⅱ必然有一個必勝的策略,也就是說對策是決定的,但在n是無窮時,對策是否是決定的就不再是明顯的事實,決定性公理是:對於每個結局集S,GS是決定的,這裡S⊆{〈p1,q1,p2,q2,…,pn,qn,…〉|pn,qn∈w}。
基本介紹
- 中文名:決定性公理
- 外文名:determinstic axiom
- 所屬學科:數學
- 所屬問題:集合論
- 簡介:公理集合論用語
基本介紹,相關說明及結論,
基本介紹
決定性公理是公理集合論用語。可添加到公理集合論ZF系統中去的一條公理,簡記為AD。其內容為:對於每一個集合S⊆N↑N,對策G(S)都是決定性的。其中的N是自然數集,N↑N是{f| f:N→N},G(S)是與集合S相關的二人對策,所謂二人對策G(S),是指:對局者甲和乙依次選取自然數:a0,b0,a1,b1,…(甲選取a0,a1,…;乙選取b0,b1,…),<a0,b0,a1,b1,…>是一個函式g:N→N,即g∈N↑N,如果g∈S,則對局者甲勝,否則為對局者乙勝。如果甲(或乙)按照某種策略g取值一定能獲勝,則稱甲(或乙)有必勝策略,並稱對策G(S)是決定性的。決定性公理與選擇公理(簡記為AC)是彼此衝突的。可以證明,在公理集合論ZFC(即ZF+AC)系統中,決定性公理不成立。反之,如果把決定性公理添加到公理集合論ZF系統中去(記作ZF+AD),則有某些弱的選擇公理成立。例如,在ZF+AD系統中,實數的非空子集的每一個可數簇都有一選擇函式。
相關說明及結論
對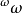 的每一個子集A,我們定義下面的遊戲GA:甲、乙二人對局,甲選取自然數a0,乙選取自然數b0,接著甲取數a1,乙取數b1,從而形成二無窮序列
的每一個子集A,我們定義下面的遊戲GA:甲、乙二人對局,甲選取自然數a0,乙選取自然數b0,接著甲取數a1,乙取數b1,從而形成二無窮序列
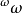
甲

乙

若所得結果序列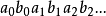 在A中,則甲勝,否則乙勝。甲的策略σ為一函式,使得對任何n,
在A中,則甲勝,否則乙勝。甲的策略σ為一函式,使得對任何n,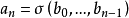 ,乙的策略
,乙的策略 也為一函式,使得對任何n,
也為一函式,使得對任何n,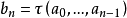 ,
,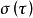 對甲(乙)來說是必勝策略,若甲(乙)運用它作遊戲GA時不管乙(甲)如何著法,他必勝。
對甲(乙)來說是必勝策略,若甲(乙)運用它作遊戲GA時不管乙(甲)如何著法,他必勝。
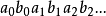
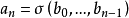

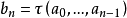
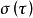
遊戲GA稱為決定的,若甲、乙二人中有一人必有必勝策略。
決定性公理(Axiom of Determinateness)
AD:對每一個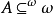 ,遊戲GA是決定的;
,遊戲GA是決定的;
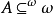
決定性公理AD與選擇公理AC不相容。
證明 設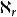 為一無窮基數使得
為一無窮基數使得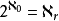 ,運用超窮遞歸構造集合
,運用超窮遞歸構造集合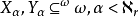 ,使得
,使得
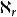
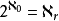
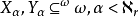
[1]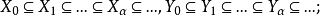
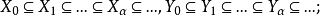
[2]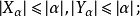
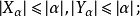
[3]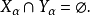
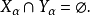
令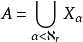 ,則A是非決定的。
,則A是非決定的。
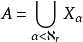
因為策略數為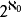 ,所以令
,所以令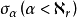 是所有策略的枚舉。設
是所有策略的枚舉。設 ,假定對所有
,假定對所有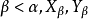 已確定。(1)若lim α,則令
已確定。(1)若lim α,則令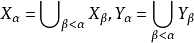 ;(2)若suc(α),令α=β+1,則
;(2)若suc(α),令α=β+1,則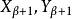 如下確定:若甲使用策略
如下確定:若甲使用策略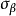 ,而乙任意地以b={b0,b1,…}與甲遊戲,則共有
,而乙任意地以b={b0,b1,…}與甲遊戲,則共有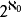 個不同的對局,以
個不同的對局,以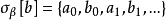 表示其中任意一個對局。因
表示其中任意一個對局。因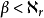 ,故存在
,故存在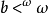 使得
使得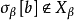 。由假定,
。由假定,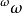 已被良序。因此我們可選取有此性質的最小b,並且
已被良序。因此我們可選取有此性質的最小b,並且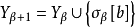 。同樣地,若乙使用策略
。同樣地,若乙使用策略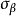 ,則存在a使得
,則存在a使得 ,這裡
,這裡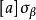 表示已使用策略
表示已使用策略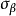 而甲取
而甲取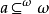 中的元與之遊戲的對局。這時選取這樣的最小a令
中的元與之遊戲的對局。這時選取這樣的最小a令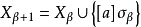 。
。
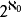
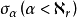

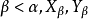
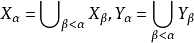
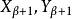
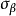
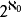
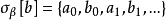
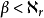
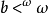
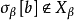
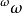
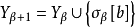
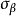

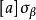
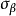
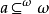
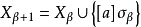
令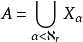 ,則我們獲得遊戲GA,因為任意策略σ是
,則我們獲得遊戲GA,因為任意策略σ是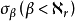 中的一個,由
中的一個,由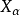 的構造可知,甲、乙二人都無必勝策略。
的構造可知,甲、乙二人都無必勝策略。
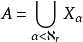
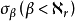
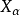
決定性公理與弱選擇公理之一——可數選擇公理是相容的。
可數選擇公理(Countable Axiom of choice):非空集的每一個可數族有選擇函式。
定理 若決定性公理成立,則實數的任一個非空子集組成的可數族有選擇函式。
證明 設X={X0,X1,...}是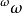 的非空子集組成的可數族,則X有選擇函式。事實上,若甲玩a={a0,a1,...}.乙玩b={b0,b1,...},甲沒有決勝策略,因為一旦甲取數a0以後,乙能容易地玩b使
的非空子集組成的可數族,則X有選擇函式。事實上,若甲玩a={a0,a1,...}.乙玩b={b0,b1,...},甲沒有決勝策略,因為一旦甲取數a0以後,乙能容易地玩b使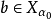 ,乙玩b={b0,b1,…},甲以{a0,0,0…}與之對局,則結果序列a0b0…
,乙玩b={b0,b1,…},甲以{a0,0,0…}與之對局,則結果序列a0b0…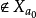 。可見乙有必勝策略
。可見乙有必勝策略 ,於是在X上定義函式f,使得f(Xn)是乙運用
,於是在X上定義函式f,使得f(Xn)是乙運用 策略時,對抗甲的{n,0,0,…}的那個b。
策略時,對抗甲的{n,0,0,…}的那個b。