基本介紹
- 中文名:水頭損失
- 外文名:head loss
- 套用學科:理工學科
- 適用領域範圍:理工學科、工業技術
- 內因:液體的粘滯性
- 定義:水流在運動過程中的機械能的損失
水頭損失的分類


計算方法
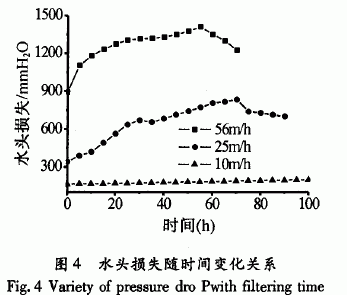 曲線1
曲線1沿程水頭損失
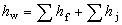 公式1
公式1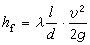 公式2
公式2 曲線2
曲線2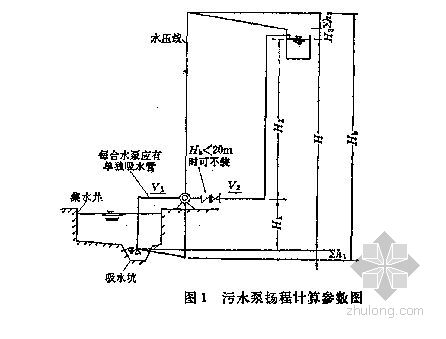 參數圖
參數圖局部水頭損失
 儀器
儀器 計算公式
計算公式 水頭損失
水頭損失


 曲線1
曲線1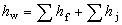 公式1
公式1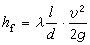 公式2
公式2 曲線2
曲線2 參數圖
參數圖 儀器
儀器 計算公式
計算公式 水頭損失
水頭損失水流在運動過程中單位質量液體的機械能的損失稱為水頭損失。產生水頭損失的原因有內因和外因兩種,外界對水流的阻力是產生水頭損失的主要外因,液體的粘滯性是產生水頭...
水流在運動過程中單位質量液體的機械能的損失稱為水頭損失。產生水頭損失的原因有內因和外因兩種,外界對水流的阻力是產生水頭損失的主要外因,液體的粘滯性是產生水頭...
局部水頭損失(local head loss)是指由局部邊界急劇改變導致水流結構改變、流速分布改變並產生旋渦區而引起的水頭損失。...
沿程水頭損失(frictional head loss)是指在固體邊界平直的水道中,單位重量的液體自一斷面流至另一斷面所損失的機械能就叫做該兩斷面之間的水頭損失。在固體邊界平...
《水頭損失計算器》是一款IOS平台的套用。...... 圖集 水頭損失計算器圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:1次歷史版本 最近更新: 創建者:美萬...
處於紊流狀態的流體在運動過程中由於受到沿程阻力的作用,會損失一部分能量,稱為紊流水頭損失。...
水輪機在工作時,水流要經過引水部件、 導水部件、轉輪和尾水管等過流部件,水流便產生摩擦、撞擊、漩渦和脫流等損失。這些情況所引起的水頭損失,稱為水力損失。它...
局部水頭損失(local loss,minor loss)發生於急變流段,用符號ζ表示。...... 局部水頭損失(local loss,minor loss)發生於急變流段,用符號ζ 表示。...
水頭損失控制儀簡稱水頭損失儀,水頭損失控制儀專用於自來水、污水處理上濾水池的檢測,可測量兩個點的液位差、水頭損失,可實現遠傳,水頭損失控制儀由水頭變送器及...
沿程損失指水流流動過程中,由於固體壁面的阻滯作用而產生的摩擦阻力所造成的水頭損失。沿程損失是隨著流程的長度而增加的。沿程阻力損失與管道長度,管內粗糙度和管...
抽水井中水流通過濾水管和在井管內運動的水流所引起的水頭損失。抽水井中的水位下降通常可表示為S=BQ+CQn...
負水頭是指在過濾過程中,當濾層截留了大量雜質以致濾層某一深度處的水頭損失超過該處水深時出現的水頭損失。...
過濾水頭損失是指水流經過濾介質及過濾設備管道時的能量損失。過濾過程中,隨著過濾時間的增加,過濾介質中截留的污染物增多,使推動過濾過程進行的水的壓力能或水的位...
亦稱“水力坡度”、“水頭梯度”。流體從機械能較大的區域向較小的區域流動時,沿流程每單位長度的水頭損失。一般用J=Δh/L表示。式中,J為水力比降,Δh為水頭...
從水力坡降求得的數據可方便地用來計算管道測試的C值(管內的粗糙係數).閥門和配件中的水頭損失(如有的話)應在計算C假之前從所觀測的壓力降中扣除,否則,巳求...
全書共分10個學習單元,內容包括:液體認知、靜水壓強與靜水壓力計算、水流運動的基本原理介紹、水頭損失計算、有壓管流水力計算、渠道水力計算、堰閘水力計算、建築物...
大量試驗表明,當滲透速度較小時,滲透的沿程水頭損失與流速的一次方成正比。在一般情況下,砂土、粘土中的滲透速度很小,其滲流可以看作是一種水流流線互相平行的流動...
一、 曼寧公式的局限性 根據謝才公式可知,謝才係數C在重力加速度為定值的情況下,謝才公式實際上與沿程水頭損失計算的通用公式一致,C僅僅受沿程阻力係數的影響。...
