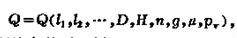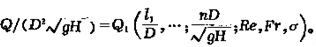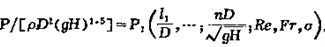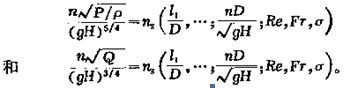水動力學實驗是液體動力學研究工作的一個組成部分。用儀器和其他實驗設備測定表征水或其他液體流動及其同固體邊界相互作用的各種物理參量,並對測定結果進行分析和數據處理,以研究各種參量之間的關係。實驗的目的是揭示各種水流運動規律和機理,驗證理論分析和數值計算結果,為工程設計和建設提供科學依據,以及綜合檢驗工程設計質量和工作狀態。 水動力學實驗是從觀測自然界和工程設施中的實際流動過程開始的,這種觀測即所謂原型實驗。進行原型實驗,難於分別控制各種參量,而且費用高,有時甚至不可能進行,如一個水利工程或水中航行器在建成前就沒有實驗對象。後來,水動力學實驗大都是在專門設計的實驗室或實驗場內用模型進行,這就是所謂模型實驗。實驗模型一般比原型小,也有與原型相等或比原型大的。水動力學模型實驗是要研究流體某一流動特性參量同邊界形狀參量、流體特性參量、作用力參量之間的函式關係。在水動力學中,有些問題可用理論分析或數值計算方法求解;有些問題因物理現象複雜,基本規律還不清楚,或因邊界形狀複雜,而只能用實驗方法研究。
水動力學實驗理論 水動力學實驗理論包括力學過程的模擬、實驗方案的最佳化、測試系統的設計、實驗數據的處理等問題。以下只論述第一個問題。
力學過程的模擬理論
水動力學實驗理論 水動力學實驗理論包括力學過程的模擬、實驗方案的最佳化、測試系統的設計、實驗數據的處理等問題。以下只論述第一個問題。力學過程的模擬理論(又稱模型理論)是模型實驗的理論依據。模型實驗的正確提法,模型實驗結果轉用到原型上去,都是以
量綱分析和
相似律為基礎的。
水動力學實驗主要涉及慣性力(見
達朗伯原理)、重力和粘性力。假定所考慮的問題可用特徵長度
L、特徵速度
U、流體密度
ρ、重力加速度
g和流體的動力粘性係數
μ來表征, 則上述三種力的數量級就分別為
、
和
μUL。三種力大小的比例關係將隨著模型尺寸而改變。但是,只有上述三種力相對大小不變,模型流動才能與原型流動相似。
根據量綱分析,在具有獨立量綱的物理參量的數目為5的情況下,可組成兩個獨立的無量綱參數。在以上所考慮的問題中,兩個獨立的無量綱參數是
弗勞德數和
雷諾數(其前者代表慣性力同重力量級之比,後者代表慣性力同粘性力量級之比。根據相似理論,若兩個流動是相似的,則兩者的所有無量綱參數的值對應相等。反之,若兩個流動中的所有無量綱參數值,包括邊界幾何參數的比值,都對應相等,則此兩個流動是相似的。在只考慮慣性力、重力和粘性力的具有幾何相似邊界的兩個流動中,若一個流動的弗勞德數和雷諾數分別等於另一個流動的弗勞德數和雷諾數,且兩個流動都是定常的(對於非定常流動,則要考慮另一個代表非定常特性的無量綱參數,如斯特勞哈爾數,它在流動中的值也應相等),則其他各無量綱參數,如壓力系
、阻力系
(
p為壓力,
D為阻力)等,在兩個流動中的值也都會相等,從而兩個流動是相似的。弗勞德數和雷諾數就是只考慮上述三種力的動力相似準數。
在水動力學實驗中,除了考慮上述三個主要力以外,有時還要考慮其他參量,例如
表面張力和聲速。在液體和氣體(或固體)的交界面上有表面張力作用在液體上。表面張力作用在液面上的壓力為:
式中
γ為表面張力(0~30℃範圍內水和空氣交界的自由面上的
γ值從0.076牛頓/米到0.071牛頓/米);
與
是自由面的兩個主曲率半徑(曲率中心在曲面外面時為正)。由上式可知,只有在液面曲率很大(曲率半徑很小)時,如在
毛細流動、
空化起始過程和漣波運動中,才要考慮表面張力。表示慣性力同表面張力量級比值的相似數是韋伯數
We:
。
為了減小表面張力不相似的影響,水動力學實驗中實驗模型縮比不能過小。
水動力學實驗中另一個相似數
馬赫數是反映流體的彈性或可壓縮性的無量綱參數,定義為:Ma=
v/
c,式中
v為流動速度;
c為流體中的
聲速。水中聲速約為1500米/秒,水動力學中經常遇到的流速比此值小很多,因此,水動力學實驗大多是不考慮馬赫數的。
當流速比較高或壓力比較低以致流場中有氣泡存在時(如
入水、
出水時),水動力學實驗中還要引進代表空泡內外壓力差(
p-
pc)的無量綱數,即空化數:
式中
p為流場內的特徵壓強;
為空泡內的壓強。當空泡中的介質主要為液體蒸氣時
pv為流場介質的飽和蒸氣壓強。當空泡中同時有氣體和液體蒸氣時,
,
為氣體分壓。空化數是表示水流是否容易發生空化的參數,空化數愈小愈容易發生空化。
水動力學實驗特點
有以下四個方面:
① 液體密度
比氣體大得多,如水的密度約為空氣的800倍。在同樣的速度下,水流的動壓力和驅動水流所需的功率也都遠大於氣流。這就要求測量水流場的儀器的支桿和感測器的某些零件有較大的
強度和
剛度。用實驗方法測量水的
附連質量是水動力學的一個重要內容。
② 液體常有和氣體交界的自由面
水體因為存在自由面而出現一些複雜現象:如風吹過水麵和艦船水面擾動;海流和潮汐運動;高速水流引起的水氣二相流;容(包括氣墊船等)在水面航行所引起的波動;魚雷和飛彈入水、出水所引起的器和明渠中的
無壓流等。在這些情況下,重力起重要作用,有時表面張力也不能忽略,又因存在粘性力,就要求在模型實驗中有兩個或兩個以上的無量綱參數同原型的相等,從而帶來不少困難。為此,常先滿足弗勞德數相等的條件,再修正其他因素的影響。
③ 液體會蒸發
當液體溫度升高、壓力降低時,蒸發速率增大,甚至出現劇烈相變現象。液體流場內某一區域壓力降低到該液體飽和蒸氣壓力(飽和蒸氣壓力同液體的種類和溫度有關,如15℃時水的飽和蒸氣壓力為0.0169大氣壓)以下,就會出現
空化現象。空化現象出現以後,流場不再是連續相,一部分為空泡所占據,這就是有空泡的流動(見
空泡流理論)。在工程上,水流(如過水壩和其他水工結構中的水流)或物體(如
水翼、船的螺旋槳和舵、水下飛彈和魚雷等)運動速度提高,就會出現空化現象和空泡流動。空化起始與空泡流動的實驗是水動力學實驗的重要內容。空泡實驗的常用設備有各種類本身的起始空化數越小越好,以便進行起始空化數小的模型實驗。降低空化數的常用方法是降低水流壓力。因此,水洞型的
水洞和變壓空化
拖曳水池。任何空化實驗設備都必須能改變空化數的值,的循環水管必須是氣密的,可抽真空,也可加壓進行深潛物體實驗。
 水動力學實驗
水動力學實驗④不能同時作到弗勞德數相似和雷諾數相似。
若模型實驗中的
g值與原型的相同,即
,當模型縮小為原型的
時(
,下標m表示模型量,p表示原型量,下同),模型速度必須降低為原型速度的
,才能保持弗勞德數
Fr不變。若模型實驗中所用的流體與原型的相同,則當模型縮小為原型的1/
kl時,模型速度必須加大為原型的
kl倍,才能保持雷諾數
Re不變。由此可見,不改變流體種類和(或)重力場就不可能做到雷諾數和弗勞德數同時相等。
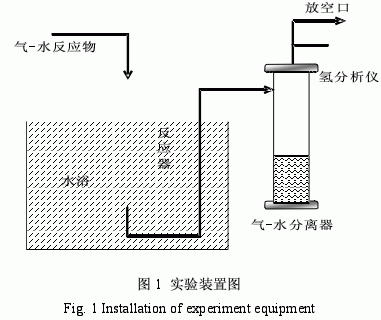 水動力學實驗
水動力學實驗很多水動力學模型實驗不能做到雷諾數相似的另一個原因是模擬對象有尺寸大於模型的特點。例如,原型船/秒,模型長度取為原型的,模型實驗介質用與原型相同的水。為了做到雷諾數相似,模型速度就必須為240節,即
m/s。為了消除在這樣的速度下將出現的空化現象(因原型中無空化現象),必須把實驗空間的壓力增加到幾十個大氣壓,這是難以做到的。對於高速船,這種情況就更嚴重。
水動力學實驗示例
以下列舉幾個實例說明水動力學實驗理論如何套用於實際。
排水量船阻力實驗 用D表示總阻力,
S表示濕面積,根據對此問題的理解,套用量綱分析方法得出,在幾何相似條件下,有下列關係:
 水動力學實驗
水動力學實驗因Fr和Re在原型和模型中相等的條件是不能同時滿足的,實驗中常維持Fr在原型和模型中相等。為了解決Re不等的問題,弗勞德近似地寫成:
式
為總阻力係數;
為當量平板摩擦阻力係數;
剩餘阻力係數。剩餘阻力包括興波阻力和粘性形狀阻力。若雷諾數超過臨界值,可以認為形狀阻力是自相似的,與雷諾數無關。於是剩餘阻力係數只是弗勞德數的函式。因
Fr值不變,故原型和模型的
CR值相等,即
。
原型和模型的
值可根據休斯曲線或ITTC(國際拖曳水池會議)曲線求出。模型的
值求出後,即可由上式計算原型的
CD值。
船和水中武器運動性能實驗 這類實驗須考慮動體的總質,轉動慣量和浮心坐標)。相似參數包這些實驗要在拖曳水池、
旋臂水池、耐波性水池、
風洞、水洞和出入水實驗室等設備內進行。
撞水實驗和入水實驗
物體從空氣中經過氣水交界面進入水中的過程稱為
入水;物體與自由水面碰撞但並不穿過水麵完全進入水中,稱為
撞水,撞水是入水的初期過程。水上飛機在水面上降落,航天飛船儀器艙和座艙在海面上濺落都是撞水的實例,而魚雷和反潛飛彈則都有入水過程。
 水動力學實驗
水動力學實驗速度不高的撞水實驗的參量有:代表撞水物體幾何形狀的具有長度量綱的幾何參量
,
,
,…和特徵長度
L,入水物體重心的坐標
、
、
,質量
m,轉動慣量
I;與撞水運動開始狀態有關的參量,如入水角
,初始攻角
,初速度
,初始角速度
;重力加速度
g,水的密度
ρ和動力粘性係數
μ。撞水和入水是非定常運動,所以還必須包括時間
t(
t=0為撞水初始瞬時)。與上述各參量對應的相似參數為:
,
,…,
;
,
,
,
;
,
,
,
,
;Fr,
Re。
因為撞水具有
衝擊性質,慣性力是主要的,雷諾數可以忽略。鈍頭物體高速撞水要考慮水和空氣的可壓縮性;模型的彈性也要作到相似。這時可忽略弗勞德數,而考慮馬赫數。
 水動力學實驗
水動力學實驗對於高速物體入水實驗,除上述相似參數外,還要考慮空泡數。入水物體尾部的空泡與一般空泡不同,前者中的氣體主要是尾隨物體沖入水中的空氣,水面上空氣的壓力pa和密度ρa是重要參量。為使空泡數不變,必須降低模型實驗中的水面壓力,但壓力一降低,水面上空氣的密度會隨著降低,從而破壞了空泡閉合過程的相似。為了做到空泡閉合過程相似,入水實驗中採用重氣體。若模型很小,為使韋伯數不比原型值小很多,常在水中加微量氣溶膠以減小表面張力。入水實驗需在專門設備中進行。
機械功率實驗
水輪機能產生多大功率、水泵需要多大功率都是重要的實驗課題。今就水輪機的功率實驗為例加以說明。設水輪機和流道的幾何形狀由長度l1,l2,…和直徑D決定;通過水輪機的流量Q除同g、μ和水頭H有關外,還同每秒轉數n有關。因為空化是水輪機運轉中的重要問題,參量中還須包括水的飽和蒸氣壓pV。流量的函式關係可寫成:
組成無量綱的參數後可得:
同樣,對於功率P可得:
和
分別稱為單位流量和單位功;
稱為單位轉速,具有表征周期運動的斯特勞哈爾數的形式。也可分別組成只包括
n、
P、
H和的兩個無量綱參數,稱為比轉速
nS,其形式分別為:
模型實驗常做不到使模型的全部無量綱參數和原型相等,有時只能維持
值相等。為了使空化數
σ相等,需要控制模型的水面壓力。因為不能滿足全部相似條件,實驗得出的模型機的效率或功率仍需用經驗公式修正才能換算到原型機。原型機的效率常高於模型機。












 水動力學實驗
水動力學實驗



 水動力學實驗
水動力學實驗
 水動力學實驗
水動力學實驗







 水動力學實驗
水動力學實驗





















 水動力學實驗
水動力學實驗