正電子湮沒譜學

正電子湮沒譜學是一種研究物質微觀結構的方法。正電子湮沒譜學已成為一種研究物質微觀結構的新手段。

基本介紹

• 中文名：正電子湮沒譜學
• 外文名：Positron Annihilation Spectroscopy， PAS
• 作用：研究物質微觀結構
• 現實用途：無損檢驗中可用來探測機械部件

介紹

一種研究物質微觀結構的方法。正電子是電子的反粒子,兩者除電荷符號相反外,其他性質（靜止質量、電荷的電量、自旋）都相同。正電子進入物質在短時間內迅速慢化到熱能區,同周圍媒質中的電子相遇而湮沒,全部質量(對應的能量為2meс2)轉變成電磁輻射──湮沒γ光子（見電子對湮沒）。50年代以來對低能正電子同物質相互作用的研究，表明正電子湮沒特性同媒質中正電子-電子系統的狀態、媒質的電子密度和電子動量有密切關係。隨著亞納秒核電子學技術、高解析度角關聯測量技術以及高能量解析度半導體探測器的發展，可以對正電子的湮沒特性進行精細的測量，從而使正電子湮沒方法的研究和套用得到迅速發展。現在，正電子湮沒譜學已成為一種研究物質微觀結構的新手段。

測量方法

實驗測量方法主要有正電子壽命測量、湮沒γ角關聯測量和湮沒譜線都卜勒增寬測量三類。

正電子壽命譜

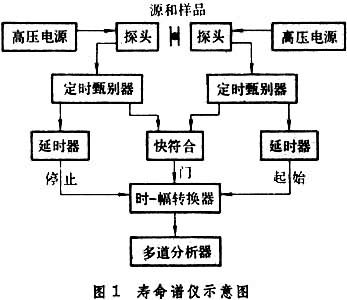
通常用22Na作正電子源,源強為幾微居里到幾十微居里。測量設備類似核能譜學中常用的符合系統，稱之為正電子壽命譜儀（見彩圖），圖1是快-快符合系統方框圖。譜儀時間解析度一般為3×10-10s左右，最好的已達1.7×10-10s。 　22Na放射的正電子入射到測試樣品中,同其中的電子發生湮沒,放出γ射線。用1.27MeV的γ光子標誌正電子的產生,並作為起始信號,511keV的湮沒輻射γ光子標誌正電子的“死亡”，並作為終止信號。兩個信號之間的時間就是正電子的壽命。在凝聚態物體中，自由正電子湮沒的平均壽命在(1～5)×10-10s範圍內。

雙γ角關聯

圖2是一維長狹縫角關聯測量系統示意圖。正電子源通常為64Cu、22Na、Co,測量時相對於固定探頭以z方向為軸轉動另一探頭,測出符合計數率隨角度的分布,就可以得到電子在某個方向上的動量分布。該方法要求高精度的機械設備和強源(幾十毫居里的點源)，典型的角解析度為0.5mrad。有些工作採用多探測器系統可作兩維動量分布的測量。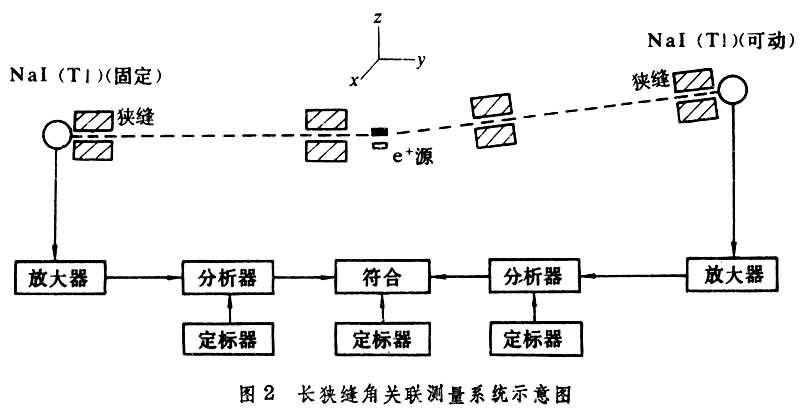

測量都卜勒增寬譜

使用高能量解析度Ge(Li)或高純鍺半導體探測器，測量湮沒輻射的能譜。能量解析度可達1keV（對85Sr,514keV的γ射線）左右。這種方法的優點是只需用幾微居里的弱源，獲取數據快，適用於動態研究。缺點是獲取的數據粗糙，對湮沒電子動量的分辨不如角關聯實驗好，典型情況下差四倍。
正電子湮沒技術可用來研究物質微觀結構及其變化。在固體物理中套用最廣泛。可用來研究晶體缺陷（空位、位錯和輻照損傷等），固體中的相變，金屬有序－無序相變等。
在無損檢驗中可用來探測機械部件(如輪機葉片、飛機起落裝置)的疲勞損傷,可在小裂縫出現之前作出預報。在化學中可用於研究有機化合物的化學反應，鑑定有機物結構中的碳正離子，研究聚合物的微觀結構等。在生物學中，研究生物大分子在溶液中的結構。醫學上，用正電子發射斷層掃瞄器，可得到人的心臟、腦和其他器官的斷面圖像，研究它們的新陳代謝過程，作出疾病的早期診斷及腫瘤的早期發現。（見彩圖）　電子偶素作為惟一的輕子體系，是驗證量子電動力學的一個理想的體系。

基本原理

自從1930年由英國物理學家P. Dirac從理論上預言了正電子的存在，以及1932年美國物理學家C.D.Anderson在宇宙射線中發現了正電子的存在以後[1]，正電子湮沒譜學(Positron Annihilation Spectroscopy，PAS)首先在固體物理中得到了套用，並在六十年代後期得到了飛速發展。它已在材料科學，特別是缺陷研究和相變研究中發揮了重大的作用。

正電子是電子的反粒子，除所帶電荷與電子相等，符號相反之外，其它特性均與電子相同。正電子進入物質後遇到電子會發生湮沒，同時放射兩個或三個湮沒g光子。用核譜學方法探測這些湮沒輻射光子，可以得到有關物質微觀結構的信息[2]。利用正電子湮沒譜學研究材料具有許多優點。它提供了一種非破壞性的探測手段，因為信息是由穿透材料湮沒輻射所帶出的。它不需要特殊的樣品製備。另外，在某些套用中，它還可以做原位研究，如在升溫過程中的化學反應動力學過程等等。實驗證明，正電子湮沒譜學是研究金屬、半導體、高溫超導體、高聚物等材料中的微觀結構、電荷密度分布、電子動量密度分布極為靈敏的工具[3-4]。

實驗方法

正電子湮沒實驗方法有如下幾種：

1)正電子湮沒壽命譜；

2)正電子湮沒輻射角關聯譜；

3)都卜勒展寬譜；

4)慢正電子束技術。

1.正電子壽命測量

正電子譜學實驗通常使用正電子源是Na，其衰變綱圖如圖3所示。伴隨著正電子發射有一個起始信號，這就是生成核Ne退激時發出的1.28MeV的g光子。正電子在樣品中湮沒後發出的能量為0.511MeV的g光子是湮沒事件的終止信號。正電子的壽命即為起始信號和終止信號之間的時間間隔，可用核電子學中的時間譜儀來測量。

正電子壽命譜儀有兩種，即快--慢符合譜儀和快--快符合譜儀。快--慢符合譜儀比較複雜，且譜儀計數率比較低。近年來人們都採用快--快符合譜儀，它具有調節方便，計數率高等優點。常用的快--快符合譜儀如圖4所示，正電子源夾在兩片相同的樣品之間，並置於兩探頭中間。探頭由BaF2晶體(或塑膠閃爍體)、光電倍增管XP2020Q及分壓線路組成。恆比定時甄別器(CFDD)具有兩種功能，既可以對所探測的g光子進行能量選擇，又可在探測到g光子時產生定時信號。調節CFDD(ORTEC 583) 的能窗，使兩探頭分別記錄同一個正電子所發出的起始和終止信號--1.28MeV和0.511MeV的光子。時間幅度轉換器TAC(ORTEC 566)將這兩個信號之間的時間間隔轉換為一個高度與之成正比的脈衝信號輸入多道分析器MCA(ORTEC 919)。MCA所記錄的即為正電子壽命譜。

2.都卜勒展寬譜

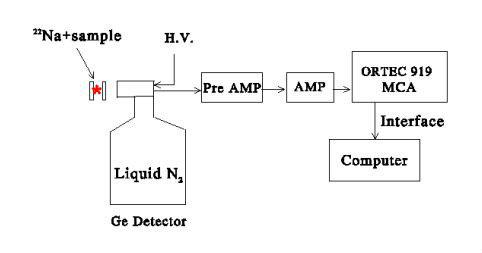
如前所述，電子--正電子對的運動會引起湮沒輻射在能量上的都卜勒移動。用高能量分辨本領的固體探測器可以探測正電子湮沒輻射的都卜勒展寬。圖5示出了都卜勒展寬譜儀的實驗裝置。源--樣品夾心結構與壽命測量中所用的相同。高純鍺探頭測到的湮沒信號經逐步放大後輸入多道分析器MCA，得到湮沒輻射的能譜。都卜勒展寬譜儀的計數率與角關聯繫統相比差不多大一百倍，收譜時間短，一般用5mCi的正電子源測量一小時就足以滿足統計精度。然而，缺點是此系統的解析度不夠高。目前Ge探測器最好的能量分辨在511KeV處為1KeV，相當於4mrad的等效角解析度，這比角關聯裝置的解析度大約差一個數量級。另外，這種系統還會出現電子學穩定性問題，因此穩譜器是必不可少的。多道分析器(ORTEC 919)所帶的數字穩譜器可以大大抑制系統的電子學漂移。

3. 慢正電子束技術（Slow Positron Beam）

前面所敘的常規正電子實驗方法利用放射源發射正電子，其能量一般都較高，而且能量分布很寬。因此只能研究塊狀材料體內的平均信息。隨著半導體技術不斷發展，材料的尺寸已越來越小，由三維發展到兩維、一微甚至零維。如何研究材料微區的結構信息已變得極為重要。

近年來發展的慢正電子束技術可以用於研究研究材料的表面和界面結構。高能正電子通過慢化體慢化後，再將其加速至所需要的能量，並利用電磁聚焦，這樣就可以得到單能慢正電子束，其能量在0～幾十keV特範圍內連續可調。如果對慢正電子進行二次慢化和再聚焦，即可得到正電子微束，可進行掃描得到材料三微結構信息。目前利用這一方法研究的材料領域已由金屬、半導體擴展到聚合物的領域，並取得了非常有意義的結果。

參考文獻

1.E. 塞格雷, 《核與粒子》, (沈子威等譯), 科學出版社(1984)
2.王少階, 《當代科技新學科》, (謝希德主編)重慶出版社,773(1993)
3.W.Brandt and A.Dupasquier(Eds.), Positron Solid-State Physics(North-
Holland, Amsterdam,1983)
4.A.Duspaquier and A.P.Mills jr.(eds) Positrons Spectroscopy of Solids
(Amsterdam, Oxford,Tokyo,Washington D.C.,1995)
5.P.J.Schulz and K.G.Lynn, Rev.Mod.Phys. 60,701(1988)
6.W.Brandt and R.Paulin, Phys.Rev.B15,2511(1977)
7.R.Paulin, in Ref.3, p565
8.P.A.M.Dirac, Proc. Camb. Phil. Soc., Math.Phys.Sci., 26, 361(1930)
9.L.I. Schiff, Quantum Mechanics, 3rd. ed(cgraw-Hill, Newyork,1961)
10.曾謹言,《量子力學》, 科學出版社(1984)