基本介紹
- 中文名:歐式蛋
- 性質:數學幾何中的一個橢圓
- 學科:數學幾何
- 提出者:羅伯特.坦肯
簡介,製作方法,
簡介
蛋光滑而勻稱,十分優美,但畫起來卻很難,要畫兩個大小和形狀一模一樣的蛋,當然更難。
而用圓規和直尺可以解決這個問題.歐氏蛋是有羅伯特.坦肯首先畫出來的。
製作方法
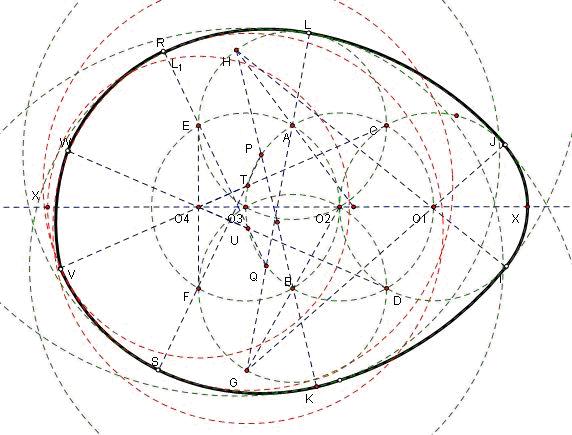
1 在MN上任取一點O1為圓心,以任意長為半徑畫圓O1與MN交於O2和X。

2 以O2為圓心,O1O2長為半徑畫圓O2,與MN交於O3.
3 以O3為圓心,O2O3長為半徑畫圓O3與圓O2交於AB。
4 以A為圓心,O2A為半徑,畫圓A,與圓O1O3分別交於CE。
5 以B為圓心,O2B為半徑,畫圓B交圓O1O3分別於DF。
6 連結O2B,並延長交圓B於G。
7 連結O2A,並延長交圓A於H。
8 連結HO1並延長交圓O1於I。
9 連結GO1並延長交圓O1於J。
10 連結HB並延長。
11 連結GA並延長。
12 以H點為圓心,HI為半徑畫弧IK,與HB延長線交於K。
13 以G為圓心,GJ為半徑畫弧JL,交GA延長線於L。
14 線段HB與圓O2交於P,連結PF並延長。
15 線段GA與圓O2交於Q,連結QE並延長。
16 以P為圓心,PK為半徑畫弧KS,與PF延長線交於S.
17 以Q為圓心,QL為半徑畫弧LR,交QE延長線於R
18 連結EF與MN交於O4
19連結CO4與圓O2交於T。
20連結DO4與圓O2交於U。
21連結TO4並延長
22 連結UO4並延長
23 以T為圓心,TS為半徑畫弧SV,交TO4延長線於V。
24以U為圓心,UR為半徑畫弧RW,交VO4延長線於W。
25以O4為圓心,O4V或O4W為半徑畫弧VW,與MN交於Y。