檢驗工作特徵

檢驗工作特徵(operating characteristic of test)亦稱檢驗操作特徵、檢驗性能特徵、檢驗操作特徵函式、檢驗OC函式。區分兩個假設的統計檢驗的重要機率。同一檢驗的操作特徵C(θ)，θ∈Θ與功效函式ω(θ)，θ∈Θ互為補余函式，即二者之和恆等於1。如，對於抽樣驗收，假設當一批產品的不合格品率為p時，接收這批產品的機率為C(p)，則C(p)，0<p<1，即該抽驗方案的工作特徵。檢驗工作特徵曲線(operating characteristic curve of test)亦稱檢驗OC曲線，簡稱OC曲線。

基本介紹

• 中文名：檢驗工作特徵
• 外文名：operating characteristic of test
• 別名：檢驗操作特徵、檢驗性能特徵等
• 簡介：區分兩個假設的統計檢驗的機率
• 所屬學科：數學（統計學）
• 定義：區分兩個假設統計檢驗重要機率

基本介紹

為了分析檢驗結果所可能犯的錯誤，A.Wald引進了所謂效函式(Power function)的概念。記

P(θ)=當參數θ為真時拒絕假設H₀的機率

=P{拒絕假設H₀/θ} (1)

上式中，θ可以取不同於θ₀及θ₁的其他參數值。常稱P(θ)為檢驗的效函式。

對於互相競擇的假設來說(記)，我們有

在實用上，往往以1-P(θ)作為檢驗中所犯錯誤的一種度量，稱它為檢驗的特性函式或OC-函式(Operating Characteristic function)，常記作L(θ)。於是：

且

L(θ)表示了當參數θ為真時採納假設H₀的機率。對於簡單假設理想的OC-函式具有下列表達形式：

它的圖形如圖1所示。

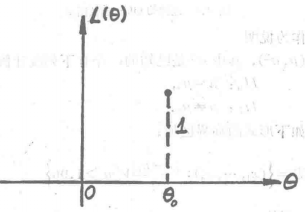圖1 理想的OC-函式圖示

表達式(5)說明了。當H₀為正確時，採納它的機率為1，當H₀為不正確的假設時，採納它的機率為0。但是，我們知道，這種理論的OC-函式在實際檢驗過程中是難於實現的(除非子樣的容量為)。雖然如此，我們可以在假設檢驗的過程中，將實際的OC-函式和理想的OC-函式進行比較，從而作出關於檢驗好壞的某種評定。從上圖可以看出，如果OC-函式所表示的曲線在近傍變化較陡，那么，所對應的檢驗也就越好。

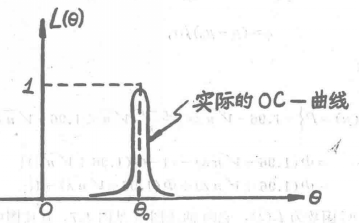圖2 實際的OC-曲線越近似於理想的OC-曲線，則檢驗有較好的性能

對於複合假設

理想的OC-曲線如下圖所示。

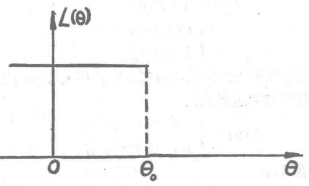圖3 理想的OC-函式圖示

舉例分析

下面舉一些例子作為說明。

例1 設，其中是巳知的，今有下列統計假設

在5%的水平下，取如下形式的臨界區域。

試確定出檢驗的OC-函式。

解： 由OC-函式的定義，知

記 ，

那么，我們有

記上述OC函式為，它的曲線圖示見圖4。在該圖中，只製作了即時的OC曲線，當時，由於為的偶函式，故圖形與縱軸對稱。

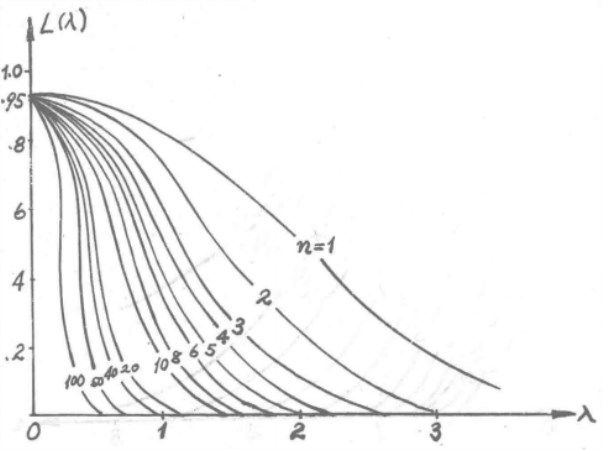
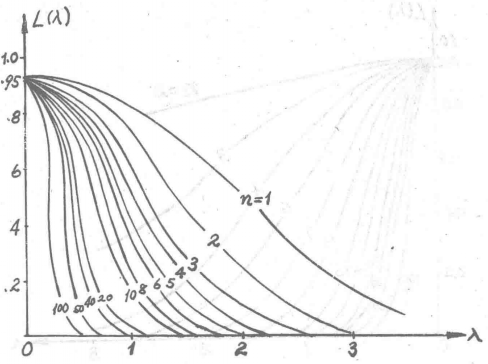圖4 OC-函式圖示

由圖4看出，當試驗次數n越大時， 曲線越陡，λ越大時，(即參數的真實值μ和μ₀的差別越大時) OC-函式的值越小。 在圖4中，如果取β=0.05, 則當n=3時，λ≌2.1，此時lμ-μ₀l=2.1σ。因此如果以距離μ₀為2.1σ的那種參數作為假設H₁時，犯第二種錯誤的機率為5%，還可以看出，當子樣的容量n>50時，OC-函式所表示的曲線其陡度並沒有顯著的改變。因此假設檢驗中犯兩種錯誤的機率並沒有多大的減少。因此考慮到試驗的費用或試驗條件的限制等等因素時，可以選定適當的試驗次數。OC-曲線有助於試驗設計中的參考。