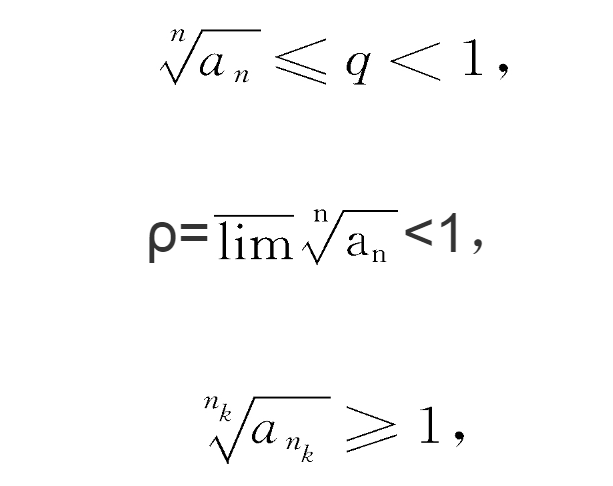檢根法

檢根法(root test)亦稱柯西判別法，是正項級數收斂與發散的一種判別法，檢根法由柯西(A.-L.Cauchy)於1821年建立。

基本介紹

• 中文名：檢根法
• 外文名：root test
• 所屬學科：高等數學
• 別名：柯西判別法，Cauchy判別法
• 簡介：正項級數收斂與發散的一種判別法

基本介紹

檢根法又稱柯西(Cauchy)判別法，是數項級數的收斂判別法，正項級數的公項u_n的n次根如果趨於一極限ρ，即

那么：

ρ<1時，級數收斂；

ρ>1或時，級數發散；

ρ=1時，檢根法失效。

檢根法的證明

證明 當ρ<1時，我們可以在ρ與1之間指定一個分數r，使不等式

成立，因為n大到m後，我們有

但又因為是收斂的等比級數(公比小於1)，所以級數

是收斂的，可知級數

也是收斂的。

當ρ>1時，所以公項不可能趨於0，因而級數發散。

當ρ=1時，仍以p級數為例，得

(因為令得，由羅彼塔第二法則得)，但是p級數可能收斂也可能發散，因此這個方法失效。證畢。

例題解析

【例1】問級數是否收斂?

解 因為

所以這個級數收斂。

【例2】討論級數的斂散性．

解 因為

由柯西判別法知級數收斂。