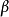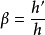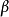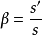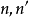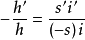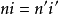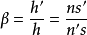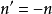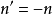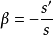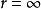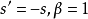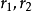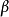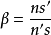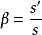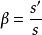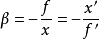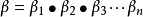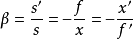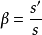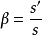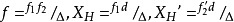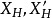橫向放大率

橫向放大率，又稱垂軸放大率，在幾何光學中具有舉足輕重的地位。我們研究光學元件及系統的成像，不僅要考慮像的位置，還要考慮其大小，橫向放大率則是聯繫物高與像高的一個重要物理量，從這個物理中我們不僅能得出像的大小，還能看出像的倒正。|β|>1 像放大，|β|<1 像縮小；β>0 像正立，β<0 像則倒立。為簡便起見，橫向放大率用β表示。

基本介紹

• 中文名：橫向放大率
• 外文名：Horizontal magnification
• 領域：光學
• 別稱：垂軸放大率
• 符號表示：β
• 相關名詞：縱向放大率

基本光學原件成像

定義為像高與物高之比，因此，該式無論對何種光學元件或系統的成像都成立，是一個普遍式。不可以什麼成像都將寫成，該式對薄透鏡成像成立，卻不能當成普遍式加以濫用。在基本光學元件成像中，即球面反射、球面折射、薄透鏡成像，球面折射為最典型的一種，其他兩種情況可以看成它的推論。

MN為一個球面，兩側分別為折射率的介質：

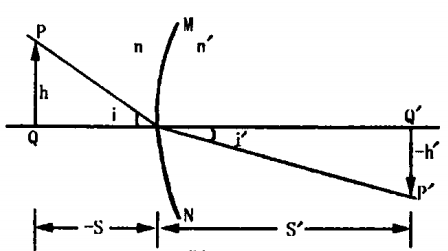
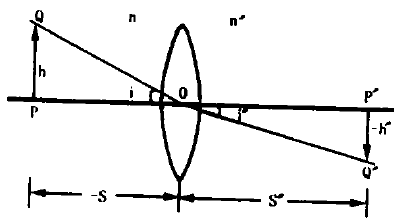
圖為球面折射：物PQ經球面折射成像為P'Q'。在近軸條件下：，又稱近軸折射定律：

因此，該式就是球面折射的橫向放大率公式。

對於球面反射的一些間題，如橫向放大率，光焦度等，許多教材上並未單獨說明。但在球面反射的情況中，物空間與像空間重合，且反射光線與人射光線的進行方向恰恰相反，對這一情況，在數學處理上可以認為，即像方介質的折射率n’等於物方介質折射率n的負值。當然，物理學中不可能存在負的折射率；倘若說有物理意義的話，則表示光線相反。因此，對於球面反射，，當然平面鏡反射也可用該式，平面鏡可看成的球面，，鏡面反射成的是等大正立虛像。

薄透鏡在教材上是單獨作為一節講述的，被作為一種常見的光學元件來研究其成像規律。薄透鏡在實質上是屬於球面折射範疇的，它可以看成是由兩個曲率半徑為的折射球面組成。

圖為薄透鏡成像，兩個折射球面的頂點可看成重合於光心O，

在該圖中，我們只考慮通過光心O的光線。現假設透鏡兩邊的折射率分別為幾n’，光線通過O點要發生折射，情況同球面折射，因此，也可寫成。由於薄透鏡通常是置於空氣中或均勻介質中n=n’，所以。至此我們應該清楚該式使用條件，如若是光學元件成像，該式適用於置於空氣中或均勻介質中的薄透鏡。另運用牛頓公式也可寫成，該式不太常用，故不詳述。

以上討論了球面折射、球面反射及薄透鏡的橫向放大率公式，應該清楚各個式子之間的內在聯繫及區別，注意它們的使用條件及範圍。

光學系統成像

實際的光學成像系統往往由兩個或兩個以上的球面(折射或及射球面)構成,若要滿足近軸條件，這些球面的曲率中心都在同一直線上,即為共軸光具組。對這類問題的成像有兩種解決方法：逐次成像法及基點法。

逐次成像法即，物點發出的光經第一球面折射的像(無論實像或虛像)即看成第二個折射球面的物，經第二個折射面成的像看成第三個折射面的物,依次下去，求出最後的像。運用這種方法，物經系統成像總的橫向放大率應為經各個元件成像的橫向放大率之乘積，即，若最後乘積為正，為正立像；乘積為負，則為倒立像。

基點法則是找一個等效的光具組來代替整個共軸光學系統，若能找出這個光具組的基點(主點、焦點)，我們就可以不逐一研究每個面成像，而用已知的高斯公式或牛頓公式計算像的位置及成像的放大率。光具組同薄透鏡的成像公式、橫向放大率具有相同形式，這正是基點法的基本思想—等效思想所致，因此，運用該公式，光具組也應置於空氣中或均勻介質中。該公式雖然形式簡單，但對初學者來說，在沒有弄清概念之前，往往容易出錯，該式中s’是以第二主點為原點，s則以第一主點為原點；同理f’以第二主點為原點，f則以第一主點為原點。因此，在使用這個式子之前，必須清楚系統的第一主點和第二主點在什麼位置，這並不是一眼就能看出來的，而是需要計算的(其中分別為系統第一主點至I系統第一主點距離，系統第二主點至11系統第二主點距離，d為I系統第二主點至11系統第一主點距離，△為光學間隔)。