基本介紹
- 中文名:機電耦合係數
- 外文名:Electro-mechanical coupling factor
- 分類:橫向縱向
- 學科:物理
- 性質:名詞
簡介
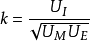


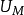
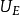
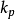

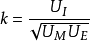


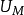
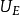
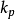
機電耦合係數意思是壓電振子在振動過程中,將機械能轉變為電能,或將電能轉變為機械能,這種表示能量相互變換的程度用機電耦合係數表示。...
機電效應又稱壓電效應,機電耦合效應。外力載入到壓電體上,外力使晶體形變,通過壓電效應把輸入的部分機械能量轉換為電能,外力所做的機械功只有一部分彈性能形式儲存...
壓電係數指的是機電耦合係數是壓電體把機械能轉變成電能或把電能轉變成機械能的轉變係數,反映壓電材料彈性性能與介電性能之間的耦合關係。壓電係數是由一個力學的...
技術上套用的壓電材料的主要性能用彈性常數、介電常數、壓電常數和機電耦合係數來標記,常簡單地合稱這些參數為壓電體的電彈常數。機電耦合係數是壓電體通過壓電...
機電耦合係數K是彈性一介電相互作用能量密度平方V122與貯存的彈性能密度V1與介電能密度V2乘積之比的平方根。 壓電陶瓷常用以下五個基本耦合係數 A、平面機電耦合...
能量轉換效率(用機電耦合係數 K33表示)高達70%,而 Ni基合金僅有16%,PZT材料僅有40~60%;其彈性模量隨磁場而變化,可調控;回響時間(由施加磁場到產生相應的應變...
60年代領先日本兩年發明銻錳鋯鈦酸鉛壓電陶瓷,突破了一般壓電陶瓷機械品質因素高機電耦合係數必然低的“常規”,獲國家發明三等獎。...
一次電光係數r12=7.0×10-12m/V,機電耦合係數R15≥0.3。為鐵電晶體,居里點(665±5)℃,自發極化強度50×10-6C/cm2。具有優良的電光、壓、電、熱釋電性能,...
67. 水永安,"2-2結構壓電複合材料的機電耦合係數研究",江蘇聲學學會成立十周年學術報告會特邀報告,199568. 水永安,薛強,"2-2結構壓電複合材料的機電耦合係數...
換能器的特性參數包括共振頻率、頻頻寬度、機電耦合係數、電聲效率、機械品質因數、阻抗特性、頻率特性、指向性、發射及接收靈敏度等等。不同用途的換能器對性能...
鈮酸鋰鐵電陶瓷屬於高溫鐵電體。居里溫度1210℃,氧八面體結構。具有優良的壓電性能,機電耦合係數和機械品質因素高,聲學傳輸損耗低,為優良傳聲介質和高頻換能器材料...
伸縮係數(×10) 1500~2000 -40 400 250 機電耦合係數 0.72 0.16~0.25 0.68 0.5~0.6 動態伸縮係數(nm/A) 1.7 -- -- -- ...
機電耦合係數大,靈敏度高;反之,靈敏度低。超音波感測器指向性 超音波感測器探測的範圍超音波感測器相關套用 編輯 超音波感測器主要套用 ...
材料科學的發展,使得套用最廣泛的壓電換能器也由天然壓電晶體發展到機電耦合係數高、價格低廉、性能良好的壓電陶瓷、人工壓電單晶、壓電半導體以及塑膠壓電薄膜等...
3.5.1壓電係數 3.5.2電容率ε(介電常數) 3.5.3頻率常數N 3.5.4電學品質因數Q。 3.5.5機械品質因數Qm 3.5.6機電耦合係數K 3.6感測器的振動模式 3.6.1壓電...
金屬梁用恆彈性係數合金材料製成,換能器用高機電耦合係數的陶瓷材料製成。在驅動換能器上輸入電信號,藉助逆壓電效應使金屬梁產生以yz平面為中性面的彎曲振動。梁...
自由介電常數、機械品質因素Qm、機電耦合係數Keff、Kp、K31、K33等,並可以繪製壓電器件的五種特性曲線(導納特性圖、阻抗特性圖、導納極坐標圖、阻抗極坐標圖、...
3Nb2/3)O3的居里溫度為-15℃,室溫下為順電體,介電常數很大,故隨著Pb( Mg1/3Nb2/3)O3含量的增加,固溶體的介電常數增大、居里溫度降低、機電耦合係數減小。...
的強各向異性的功能性陶瓷,其介電性、壓電性和彈性等物理性質都表現出明顯的各向異性,同時,用以表征晶體的彈性性能與介電性能之間耦合程度的機電耦合係數K也具有...
經人工高壓極化具有壓電 性,其機電耦合係數(Kp) 0.36,品 質因數(Qm) 300,壓電常數d31和d33分別達-80×10-12C/N和190× 10-12C/N,居里溫度120℃,用於...
機電耦合係數大,靈敏度高;反之,靈敏度低。超音波距離感測器結構工作原理 編輯 當電壓作用於壓電陶瓷時,就會隨電壓和頻率的變化產生機械變形。另一方面,當振動壓電...
(3)靈敏度。主要取決於製造晶片本身。機電耦合係數大,靈敏度高;反之,靈敏度低。如超音波感測器,一個複合式振動器被靈活地固定在底座上。該複合式振動器是諧振器...
