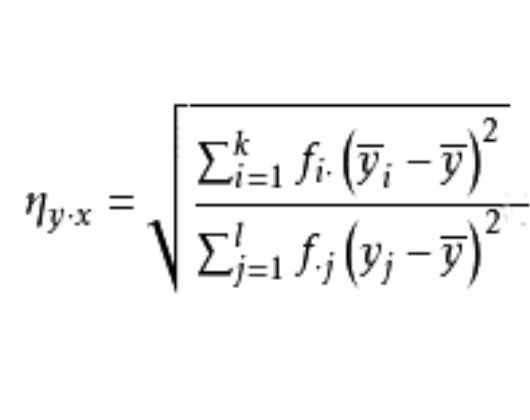樣本相關比(sample correlation ratio)是與相關比對應的樣本特徵,樣本可決係數(或樣本復可決係數)的平方根。樣本相關比是根據樣本數據計算的兩個變數間某一變數對另一變數不以直線為準的相關程度的係數。 相關比是曲線相關的指標,從變數觀測值的分布情況或散點圖上看,兩變數沒有直線關係而呈現曲線趨勢時,不可以計算積矩相關係數,應當計算兩變數的相關比作為其曲線相關程度的指標。
基本介紹
- 中文名:樣本相關比
- 外文名:sample correlation ratio
- 所屬學科:數學(統計學)
- 簡介:曲線相關的指標
- 提出者:K·皮爾生
基本介紹
x1 | … | xi | … | xk | 合計 | |
y1 | f11 | … | fil | … | fkl | f·1 |
… | … | … | … | |||
yj | f1j | … | fij | … | fkj | f·j |
… | … | … | … | |||
yl | f1l | … | fil | … | fkl | f·l |
合計 | f1· | fi· | fk· | n |