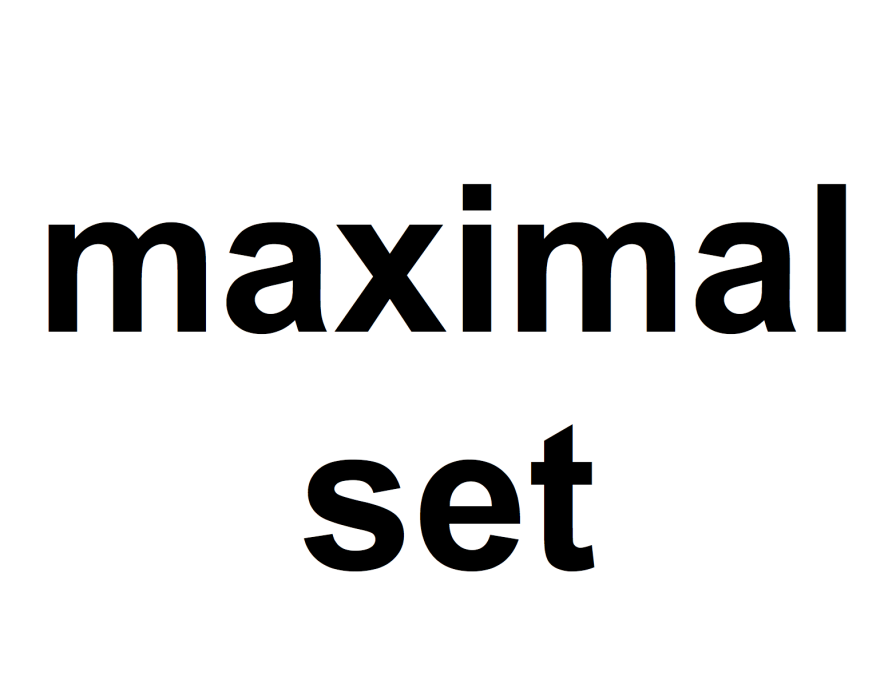定義
發展
弗里德貝格(Friedberg,R. M.)於1958年證明了極大集的存在性,並證明了極大集都是hh單純集。因而,極大集概念是hh單純集的進一步加強。
耶茨(Yates , C. E. M.)於1965年證明存在一個T完全的極大集。
極大集的存在不足以肯定回答波斯特問題。注意到從單純集、h單純集、hh單純集到極大集,它們補集的元素越來越“稀疏”。而極大集之補的元素已是最稀疏的了,但這仍不足以保證其非T完全性,即用限制其補集元素之“稀疏性”的辦法是無法解決波斯特問題的。
實際上,
波斯特問題的解決是由弗里德貝格和穆切尼克(Mucnik,A. A.)用有窮損傷優先方法解決的。
內聚集
內聚集是一種特殊的禁集。如果自然數 A 是無窮的,且不能被任何
遞歸可枚舉集分成兩個無窮部分,即對任何遞歸可枚舉集
和
中至少有一個是有窮的,則稱 A 是內聚集。