棘齒系統

棘齒系統熱力學平衡的破壞和某種對稱性的破缺。在熱力學平衡態下，外力總效果為零的系統出現定向運動意味著第二類永動機(單源熱機)，違反了熱力學第二定律。在實際套用中，熱力學平衡的破壞往往通過加驅動或噪聲來實現。不滿足反演對稱性的周期勢在物理學中稱為棘齒勢。棘齒勢在研究定向輸運問題中被廣泛套用，它滿足產生定向輸運的第二個條件——對稱性破缺。能夠產生定向輸運的系統在物理上稱為棘齒系統，在生物上稱為分子馬達。

基本介紹

• 中文名：棘齒系統
• 外文名：Ratchet system
• 性質：系統
• 作用：熱力學平衡
• 學科：物理

概念

棘齒系統(分子馬達)的研究，最早源自於熱力學中有關第二類永動機問題的爭論。棘齒系統能夠從漲落(噪聲)或非定向驅動中吸收能量並將之轉化為定向運動的能量(做功)。因此早期的棘齒系統往往有噪聲存在。後來人們發現，在缺少噪聲的情況下仍有可能存在定向輸運(確定性棘齒)。由於計算量的原因，一開始人們研究的大多是比較簡單的過阻尼系統。後來隨著計算技術的發展，對非過阻尼系統(慣性棘齒)的研究逐漸豐富起來。

確定性慣性棘齒系統的定向輸運

研究背景

定向輸運問題一直受到物理、生物等諸多領域的密切關注。一般的定向輸運的特點是：產生定向輸運需要一個空間上的定向外場，或者說需要受到平均效果在某一方向上不為零的力的驅動。這種定向輸運的研究已經進行了很長時間並且相對成熟，現象為大多數人所熟知和了解，其機制和結論也很容易理解。另外一種機制的定向輸運受到了廣泛的關註：系統受到的外力的總效果為零，即受力沒有任何的偏向卻出現了沿某一方向的定向輸運現象。研究的結果表明，這樣的系統需要滿足兩個條件：熱力學平衡的破壞和某種對稱性的破缺。

圖1 無量綱周期棘齒勢

關於棘齒系統(分子馬達)的研究，最早源自於熱力學中有關第二類永動機問題的爭論。棘齒系統能夠從漲落(噪聲)或非定向驅動中吸收能量並將之轉化為定向運動的能量(做功)。因此早期的棘齒系統往往有噪聲存在。後來人們發現，在缺少噪聲的情況下仍有可能存在定向輸運(確定性棘齒)。由於計算量的原因，一開始人們研究的大多是比較簡單的過阻尼系統。後來隨著計算技術的發展，對非過阻尼系統(慣性棘齒)的研究逐漸豐富起來。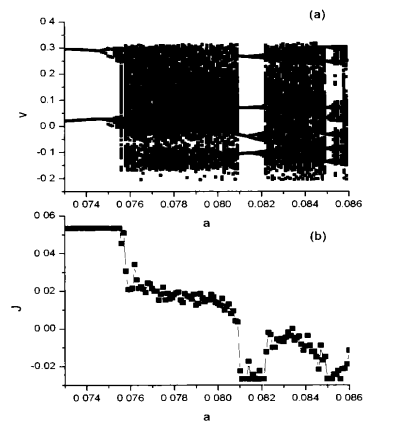

圖2 (a)相應於參數a的分叉圖，(b)定向流J

在2000年墨西哥的Mateos在國際物理刊物《物理評論快報》(Physical Review Letters)發表了一篇名為《確定性棘齒系統中的混沌輸運和反向流》的文章，接著義大利的Barbi和Salerno在Physical Review E中對Mateos的結論提出了不同的看法。在這篇文章中，我們將使用他們的模型，研究對比相同形狀但高度不同的確定性慣性棘齒下的定向輸運。

模型

考慮一維情況，在一般阻尼下，處於非對稱周期勢中的單粒子在周期外力驅動下的運動。無量綱化之後的粒子的動力學方程為

上式中，b是摩擦係數，ω是驅動的頻率，a是驅動的振幅。非對稱周期勢定義為

在本文中，δ取兩個值：δ₁=sin(2πx₀)+sin(4πx₀)=1.614，δ2=sin(2πx₀)+sin(4πx₀)4 =1.101。x₀=-0.19使得勢在x =0位置有一個勢能最低點，C=0.0173使得當δ=δ₁時勢能最低點V(0)=0，見圖1。

在第一個方程中有3個無量綱參量：a，b和ω。在本文中，我們將在不同的參數a下對粒子的運動進行比較，而把參數b和ω固定，b=0.1，ω=0.67，δ=δ₁是參考文獻所採用的模型。

圖3 (a)a =0.074(正向流)，(b)a=0.081(反向流)

在不同參數下粒子的運動可能是周期的也可能是混沌的。研究混沌運動的粒子的平均速度有兩種方法，一種是長時平均，一種是系綜平均。本文採用的是第一種方法，長時平均

本文的數值模擬使用四階龍格-庫塔方法接常微分方程，積分步長為T_ω/1000，其中Tω為外加驅動周期T_ω=2π/ω。

數值結果

參考文獻研究了δ=δ₁，a∈[0.073，0.086]粒子的定向流和相應的分叉圖(圖2)。該文的作者發現了沿正方向運動的周期二軌道，見圖3(a)，和沿反方向運動(逆向流)的周期四軌道，見圖3(b)。

圖4 (a)相應於參數a的分叉圖，(b)定向流J和a的關係

作者計算了δ=δ₂，a∈[0.073，0.086]粒子的運動，發現雖然兩者的棘齒勢只有高度的差別，但是在同樣參數下粒子的運動卻有很大的差別，見圖4。當δ=δ₁，a=0.074出現的正向流和a=0.081出現的反向流，在δ=δ₂的情況下消失不見。原來圖2中明顯的倍周期分叉現象也沒有了。

後來我們仔細研究了a=0.074和0.081時粒子的運動，發現從某些初值出發的暫態過程經歷了類似的周期定向運動，而後才到達不動的周期振盪解。由此可以判斷，原來δ=δ1，a=0.074時存在的穩定的沿正方向運動的周期二解和a=0.081時存在的穩定的沿反方向運動的周期四解，當δ=δ2時失穩，取而代之的是穩定的不動的周期振盪解。在a∈[0.07601，0.07955]，系統同時存在兩個穩定的周期解，沿正方向運動的周期二解和不動的周期振盪解。粒子從不同的初始條件出發會落到不同的周期軌道上。

棘齒系統中的周期吸引子共存現象

研究背景

棘齒系統中的定向輸運現象引起了廣泛的關注。棘齒系統定向輸運研究的是在外力總效果為零(甚至沒有外力)時產生定向輸運的可能性與機制。其在諸多領域中皆有套用，像生物領域中的分子馬達，粒子分離，以及量子領域中的棘齒效應等。最早人們希望從噪聲中提取有用的功。後來人們發現沒有噪聲的情況下定向輸運仍然可能發生。在考慮粒子慣性的情況下，確定性棘齒系統表現出複雜的動力學，甚至確定性混沌可以在一定程度上扮演噪聲的角色。

定向輸運的方向一般由棘齒系統的非對稱性決定，因而有其特定的自然方向。但是，人們又發現一些特定系統參數下，定向輸運的方向並不是自然方向，即流發生了反轉(current reversal)。流反轉是一個很有趣並且值得討論的事情。為了研究它，人們做了很多工作，但其內在的機制一直沒被發現。

研究進展

文獻指出了系統不僅存在混沌吸引子，也存在周期吸引子，並且指出了在特定參數下周期通向混沌的道路是通過分岔實現的，與此同時流發生了逆轉，文獻在更大參數範圍內對系統進行了模擬，結果表明流逆轉的同時分岔並不一定發生。作者在此基礎上的研究發現相同參數下兩個周期吸引子可以共存，並提出流反轉是由於不同周期吸引子的穩定性引起的。本文則是在文獻的基礎上，對系統隨參數a的變化進行了更加細緻的研究。

圖5 定向流隨驅動振幅a的變化

圖5中我們畫出了不同振幅a驅動下系統從不同初始條件出發可能出現的定向流的值，從圖中可以看到，在一個很小的參數範圍內，系統先後經歷了多種周期吸引子存在狀態。當a∈[1.27，1.274]，系統只存在1個J =-v_ω的周期吸引子；a =1.275，系統中J=-v_ω與J=0兩個周期吸引子共存；a∈[1.276，1.282]，系統中J=±v_ω與J =0，3個周期吸引子同時存在；a∈[1.283，1.30]，系統中J=±v_ω兩個周期吸引子共存。3個吸引子共存的現象是文獻沒有提及的。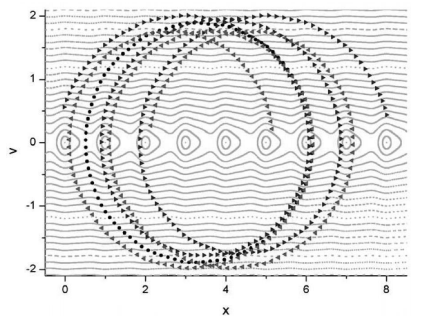

圖6 a=1.276時系統中同時存在3個周期吸引子

在圖6中我們畫出了a=1.275時系統同時存在的3個吸引子的軌跡。圖中背景為未受擾動時系統的相圖，灰色線即為等能線。黑色圓圈描述了J=0的軌道，可以看到粒子在驅動下先向右越過6個棘齒勢周期，接著向左越過6個棘齒勢周期回到原來的地方。藍色右三角描述了J=v_ω的軌道，粒子先向右運動越過6個棘齒勢周期，接著向左運動5個棘齒勢周期，從而在一個驅動周期內實現了向右運動1個棘齒勢周期。紅色左三角描述的J=-v_ω軌道則剛好相反，粒子先向右運動了5個棘齒勢周期，接著向左運動6個棘齒勢周期，從而每個驅動周期粒子將向左運動1個棘齒勢周期。為了更清楚地觀察這3個周期吸引子，我們畫出了它們的軌道隨時間變化的3維示意圖，見圖7。圖中，z軸為時間。可以很清楚地看到，3個吸引子都是周期1的。

此外，就如圖6和7中所表現的，3個吸引子靠得很近。也就是不需要太大的擾動就可以將系統從一個周期吸引子軌道上驅動到另一個周期吸引子軌道上。比如，當初始速度固定為零，初始位置分別為0.24，0.25和0.26，則系統將分別進入J=0，J=-v_ω和J=v_ω的周期軌道上，即圖7中的(a)，(c)和(b)。

研究結論

我們研究了一個確定性欠阻尼棘齒系統，在系統中不僅兩個周期吸引子可以共存，甚至3個周期吸引子也可以同時存在。我們刻畫了系統共存的3個吸引子的軌道，並指出它們之間的距離比較近，系統比較容易受到擾動而從一個周期軌道跑到另一個軌道上。