梳排序（Comb sort）是一種由Wlodzimierz Dobosiewicz於1980年所發明的不穩定排序算法，並由Stephen Lacey和Richard Box於1991年四月號的Byte雜誌中推廣。梳排序是改良自泡沫排序和快速排序，其要旨在於消除烏龜，亦即在數組尾部的小數值，這些數值是造成泡沫排序緩慢的主因。相對地，兔子，亦即在數組前端的大數值，不影響泡沫排序的性能。
在泡沫排序中，只比較數組中相鄰的二項，即比較的二項的間距（Gap）是1，梳排序提出此間距其實可大於1，改自插入排序的希爾排序同樣提出相同觀點。梳排序中，開始時的間距設定為數組長度，並在循環中以固定比率遞減，通常遞減率設定為1.3。在一次循環中，梳排序如同泡沫排序一樣把數組從首到尾掃描一次，比較及交換兩項，不同的是兩項的間距不固定於1。如果間距遞減至1，梳排序假定輸入數組大致排序好，並以泡沫排序作最後檢查及修正。
基本介紹
- 中文名：梳排序
- 外文名：Comb sort
- 領域：計算機編程
- 目標：消除烏龜，在陣列尾部的小數值
- 含義：不穩定排序算法
- 提出者：Wlodzimierz Dobosiewicz
- 提出時間：1980
- 推廣者：Stephen Lacey和Richard Box
- 推廣方式：1991年四月號的Byte雜誌
介紹,排序算法,遞減率,變異形式,梳排序-11,混合梳排序和其他,偽代碼,算法實現,動作原理,參看,
介紹
梳排序（Comb sort）是一種由Wlodzimierz Dobosiewicz於1980年所發明的不穩定排序算法，並由Stephen Lacey和Richard Box於1991年四月號的Byte雜誌中推廣。梳排序是改良自泡沫排序和快速排序，其要旨在於消除烏龜，亦即在數組尾部的小數值，這些數值是造成泡沫排序緩慢的主因。相對地，兔子，亦即在數組前端的大數值，不影響泡沫排序的性能。
在泡沫排序中，只比較數組中相鄰的二項，即比較的二項的間距（Gap）是1，梳排序提出此間距其實可大於1，改自插入排序的希爾排序同樣提出相同觀點。梳排序中，開始時的間距設定為數組長度，並在循環中以固定比率遞減，通常遞減率設定為1.3。在一次循環中，梳排序如同泡沫排序一樣把數組從首到尾掃描一次，比較及交換兩項，不同的是兩項的間距不固定於1。如果間距遞減至1，梳排序假定輸入數組大致排序好，並以泡沫排序作最後檢查及修正。
排序算法
在計算機科學與數學中，一個排序算法（英語：Sorting algorithm）是一種能將一串數據依照特定排序方式進行排列的一種算法。最常用到的排序方式是數值順序以及字典順序。有效的排序算法在一些算法（例如搜尋算法與合併算法）中是重要的，如此這些算法才能得到正確解答。排序算法也用在處理文字數據以及產生人類可讀的輸出結果。基本上，排序算法的輸出必須遵守下列兩個原則：
- 輸出結果為遞增序列（遞增是針對所需的排序順序而言）
- 輸出結果是原輸入的一種排列、或是重組
雖然排序算法是一個簡單的問題，但是從計算機科學發展以來，在此問題上已經有大量的研究。舉例而言，冒泡排序在1956年就已經被研究。雖然大部分人認為這是一個已經被解決的問題，有用的新算法仍在不斷的被發明。
遞減率
遞減率的設定影響著梳排序的效率，原作者以隨機數作實驗，得到最有效遞減率為1.3的。如果此比率太小，則導致一循環中有過多的比較，如果比率太大，則未能有效消除數組中的烏龜。
亦有人提議用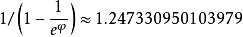
作遞減率，同時增加換算表協助於每一循環開始時計算新間距。
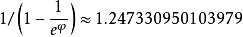
因為程式語言中乘法比除法快，故會取遞減率倒數與間距相乘，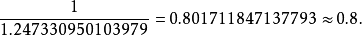
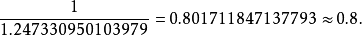
變異形式
梳排序-11
設定遞減率為1.3時，最後只會有三種不同的間距組合：(9, 6, 4, 3, 2, 1)、(10, 7, 5, 3, 2, 1)、或 (11, 8, 6, 4, 3, 2, 1)。實驗證明，如果間距變成9或10時一律改作11，則對效率有明顯改善，原因是如果間距曾經是9或10，則到間距變成1時，數值通常不是遞增序列，故此要進行幾次泡沫排序循環修正。加入此指定間距的變異形式稱為梳排序-11(Combsort11)。
混合梳排序和其他
此方法的最大好處是不再需要檢查有否進行過交換程式以將排序循環提早結束。
偽代碼
梳排序程式（以array作輸入） gap = array的長度//設定開始時的間距 當gap > 1或swaps = 1時執行迴圈//代表未完成排序 gap =取「gap除以遞減率」的整數值//更新間距 swaps = 0 //用以檢查陣列是否已在遞增形式，只限gap=1時有效 //把輸入陣列「梳」一次 i = 0到(array的長度- 1 - gap)來執行迴圈//從首到尾掃描一次；因為陣列元素的編號從0開始，所以最後一個元素編號為長度-1 如果array[i] > array[i+gap] 把array[i]和array[i+gap]的數值交換 swaps = 1 //曾作交換，故此陣列未必排序好 如果結束 迴圈結束 迴圈結束程式結束
算法實現
C語言實現：
void comb_sort(int* data, int n){const double shrink = 1.25;int i, delta = n, noswap = 0;while(!noswap){for(noswap = 1, i = 0; i + delta < n; i++)if(data[i] > data[i + delta]){data[i] ^= data[i + delta];data[i + delta] ^= data[i];data[i] ^= data[i + delta];noswap = 0;}if(delta > 1){delta /= shrink;noswap = 0;}}}動作原理
假設輸入為
- 8 4 3 7 6 5 2 1
目標為將之變成遞增排序。因為輸入長度=8，開始時設定間距為8/1.3≒6，則比較8和2、4和1，並作交換兩次。
- 84 3 7 6 521
- 243 7 6 5 81
- 2 1 3 7 6 5 8 4
第二次循環，更新間距為6/1.3≒4。比較2和6、1和5，直至7和4，此循環中只須交換一次。
- 2 1 376 5 84
- 2 1 3 4 6 5 8 7
接下來的每次循環，間距依次遞減為3 → 2 → 1，
間距=3時，不須交換
- 2 1 3 4 6 5 8 7
間距=2時，不須交換
- 2 1 3 4 6 5 8 7
間距h=1時，交換三次
- 213 4 6 5 8 7
- 1 2 3 4658 7
- 1 2 3 4 5 687
- 1 2 3 4 5 6 7 8
上例中，共作了六次交換以完成排序。
參看
- 泡沫排序，梳排序的基本，較慢的算法。
- 雞尾酒排序，或雙向泡沫排序，一樣解決了泡沫排序中的烏龜問題。
