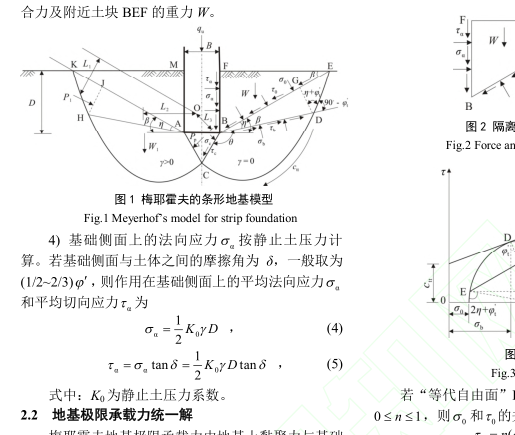
梅耶霍夫極限承載力公式是由G. G.梅耶霍夫推導的地基極限承載力公式，將太沙基承載力理論加以發展，認為應考慮基礎兩側土體的抗剪強度，並使地基土的塑性平衡區擴展到基礎埋置深度以上的土中。梅耶霍夫還研究了深基礎的極限承載力以及基礎受偏心荷載和傾斜荷載的承載力。
基本介紹
- 中文名：梅耶霍夫極限承載力公式
- 外文名：Meyer Hoff's formula for ultimate bearing capacity
- 學科：土力學
- 提出者：梅耶霍夫
- 基礎理論：太沙基承載力理論
- 有關術語：地基承載力
簡介,假設,太沙基承載力理論,地基承載力,
簡介
1951年梅耶霍夫對太沙基理論做了進一步的改進，即考慮了基底以上土體的剪下強度對地基極限承載力的影響。在淺基礎的地基極限承載力計算中，將基礎兩側底面以上的土層簡單當作荷載，忽視作為過載土層的抗剪強度，這無疑會低估地基的承載力。在基礎埋深較淺的情況下，作為過載的土層的抗剪強度也相對較小，忽略其對地基承載力的影響所造成的誤差也較小。若基礎埋置深度較大；但仍採用淺埋基礎的影響，把基底以上土層簡單地作為荷載，這顯然會帶來較大誤差，梅耶霍夫在計算地基土的極限承載力公式中，考慮了基底以上土的抗剪強度這一因素。對於均質地基，用簡化方法導得條形基礎在中心荷載作用下的地基極限承載力公式
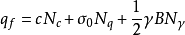
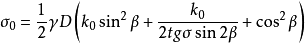
式中c為土的粘聚力；γ為土的重度；D、B分別為基礎的埋深和寬度；為等代自由面上的法向應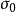
力；β為等代自由面與水平面的傾角；
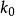為靜止土壓力係數；δ為土與基礎側面之間的摩擦角；
、
、
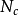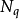為與土的內摩擦角φ和β角有關的承載力係數。
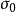
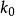
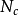
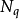
假設
梅耶霍夫理論假定如下：基礎底面完全粗糙，條形地基為整體剪下破壞，地基土為均質非飽和土，且地下水位處於地基滑動面以下，基質吸力沿深度均勻不變；滑動面上的土體處於塑性極限平衡狀態。基礎側面上的法向應力按靜止土壓力計算。梅耶霍夫地基極限承載力由地基土黏聚力與基礎旁側荷載、滑動土體自重與被動土壓力等提供，採用剛塑性體的極限平衡法，根據線性疊加原理進行公式推導。在計算地基土黏聚力與基礎旁側荷載所提供的承載力時，用“等代自由面”BE 上的法向應力和切向應力來反映基礎旁側土抗剪強度的影響，這種處理方式更符合實際情況。
太沙基承載力理論
K·太沙基假設基底粗糙並考慮土自重影響導 出的地基極限承載力理論。於1943年提出，1967 年作了局部修改，該理論將普朗德爾承載力理論套用到地基極限承載力課題。基本假定1）地基和基礎之間的摩擦力很大（地基底面完全粗糙），當地基破壞時，基礎底面下的地基土楔體aba′（如圖8-7所示）處於彈性平衡狀態，稱彈性核。邊界面ab或a′b與基礎底面的夾角等於地基土的內摩擦角φ。2）地基破壞時沿bcd曲線滑動。其中bc是對數螺線，在b點與豎直線相切；cd是直線，與水平面的夾角等於45°-φ/2 ，即acd區為被動應力狀態區。3）基礎底面以上地基土以均布荷載q=γD代替，即不考慮其強度。
地基承載力
地基承載力是指通過計算分析確定地基所能承受的極限荷載。地基承載力是經典土力學及岩土工程的一個重要課題，合理確定地基承載力對工程的安全性和經濟性均具有重要意義。1920年，普朗德爾首先根據極限平衡理論導出了條形基礎的極限承載力計算公式。假定基礎底面與土之間是光滑的、基礎下土是無重量的介質，滑動面是由兩組平面及中間過渡的對數螺旋曲面組成。假定條件與實際不符，故其結果是粗略的。20世紀40年代太沙基在普朗德爾理論基礎上提出考慮土自重的極限承載力公式。20世紀50年代梅耶霍夫提出了適用於深基礎的極限承載力公式，土中滑動面可以延伸到基礎底面以上，但求解時還存在著數學上的困難。地基的極限承載力是地基內部整體達到極限平衡時的荷載。求解極限荷載的方法有兩種： 1. 根據極限平衡條件建立微分方程，根據邊界條件求出地基整體達到極限平衡時各點的精確解。由於這一方法只對一些簡單的條件得到了解析解，其它情況則求解困難，故不常用。2. 假定滑動面法，然後以滑動面所包圍的土體作為隔離體，根據靜力平衡條件求解。這種方法概念明確，計算簡單，得到廣泛套用。 極限平衡理論是研究土體處於理想塑性狀態時的應力分布和滑裂面軌跡的理論。它不僅用來求解地基的極限承載力和地基的滑裂面軌跡，也可以求擋土牆土壓力、邊坡的滑面軌跡等有關土體失穩所涉及的問題。由於這種理論分析方法解題複雜，但對於求解地基極限承載力，這種方法則是主要的理論基礎。 在理想彈一塑性模型中，當土體中的應力小於屈服應力時，應力和變形用彈性理論求解，這時土體中每一點都應滿足靜力平衡條件和變形協調條件。當土體處於塑性狀態時應滿足極限平衡條件。
