格羅蔣茨圖(Grotzsch graph)是一種特殊的圖。一個4色臨界圖的例子。極圖是一類特殊的圖。指階數一定在某種意義下最大的圖。給定一個圖族L,在所有n階圖中含邊最多,不以L中圖為其子圖的圖。
基本介紹
- 中文名:格羅蔣茨圖
- 外文名:Grotzsch graph
- 領域:數學
- 性質:4色臨界圖
- 本質:極圖
- 提出者:格羅蔣茨
概念,色臨界圖,極圖,格雷圖,
概念
格羅蔣茨圖(Grotzsch graph)是一種特殊的圖。一個4色臨界圖的例子(見圖)。
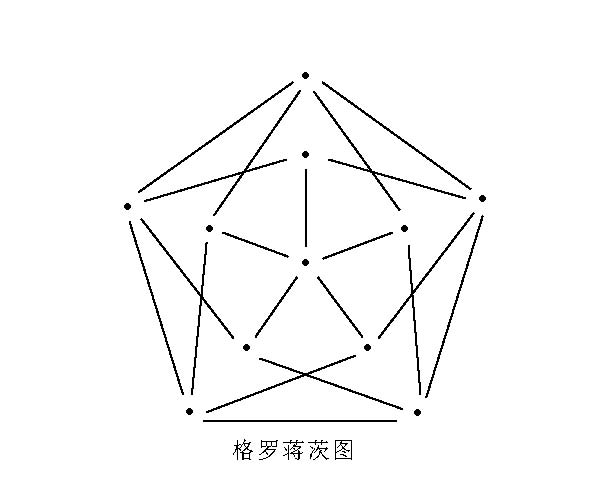 格羅蔣茨圖
格羅蔣茨圖色臨界圖
亦稱點著色臨界圖。一類與色數有關的極圖。圖G為色臨界圖是指:若對於G上任一節點v,有χ(G-v)<χ(G),其中,χ(X)表示圖X(X=G-v或G)的色數。稱圖G為邊色臨界圖,若對G的任一邊x,圖G-x的邊著色數:
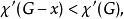
極圖
極圖是一類特殊的圖。指階數一定在某種意義下最大的圖。給定一個圖族L,在所有n階圖中含邊最多,不以L中圖為其子圖的圖。這個給定的圖族L稱為禁用圖類。關於L的全部n階極圖的集記為Ex(n,L),其中每個極圖邊數相等,記為ex(n,L)。例如,Tm,n圖,即有n個節點,各部節點數分別為[n/m](即n/m的整數部分)或[n/m]+1的完全m部圖,就是一個極圖。其中,L是m+1階完全圖。Tm,n常稱為圖蘭圖。事實上,有圖蘭定理:在所有不含完全圖Kn作為子圖的m階圖中,邊數最多的圖只有一個,就是Tm,n-1。它第一次出現在圖蘭(Turn,P.)1941年發表的文章中,由此而得名。
格雷圖
格雷圖是一種特殊的圖。指一個有54個頂點(較福克曼圖多)的3正則的邊可遷但非頂點可遷的圖。它是這樣構造的:三個K3,3圖,每個的九條邊一一對應,每一對應的三邊組中加一個剖分點,如圖中v1,v2,v3,然後另加一點v4與此三點相連。下面的圖只畫出其中一組。
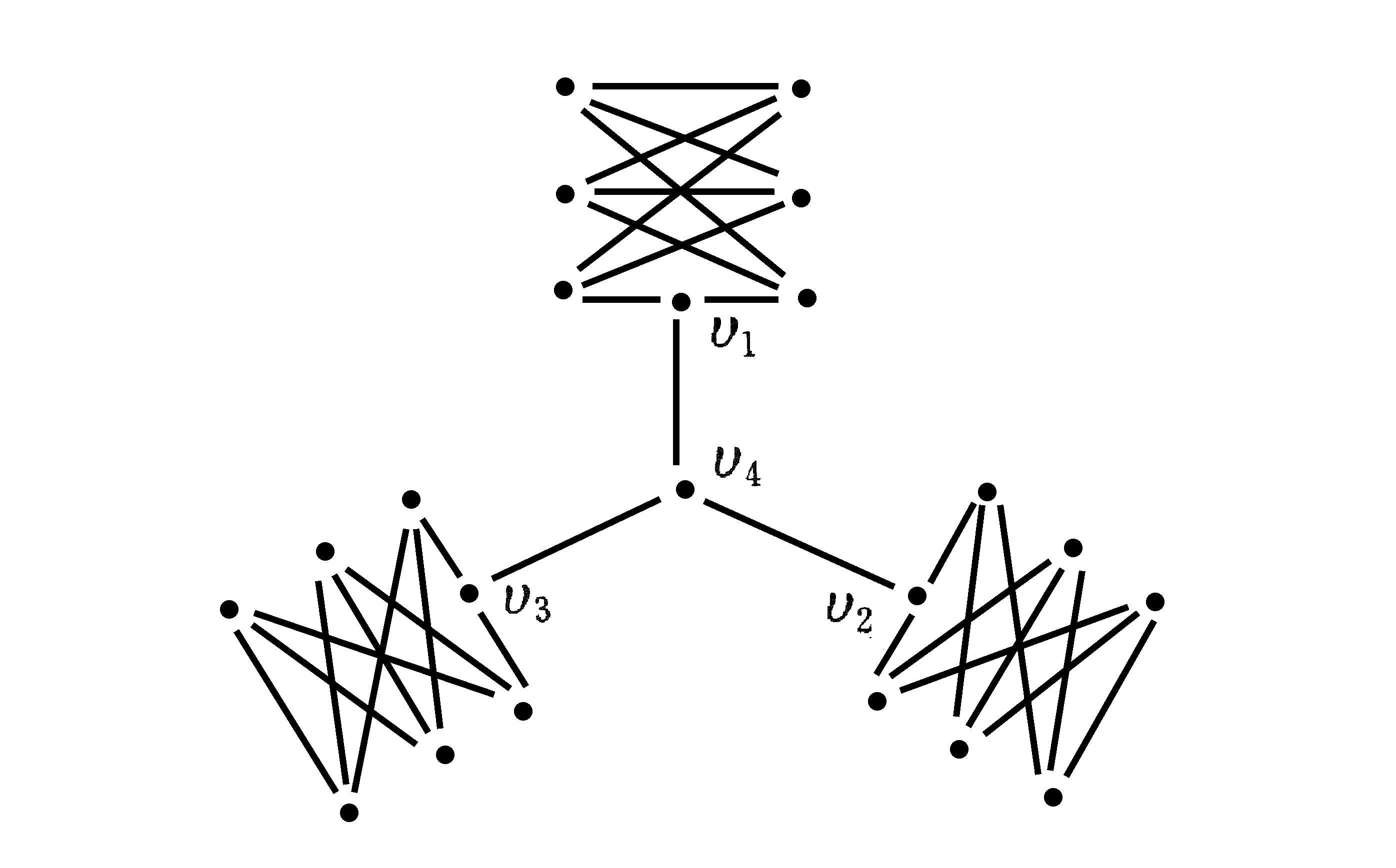 格雷圖
格雷圖
