格林線

設區域D的格林函式為G(x,a)，a為D中某個取定的點，那么它的正交軌線稱為格林線。

基本介紹

• 中文名：格林線
• 外文名：Green line
• 適用範圍：數理科學

簡介

格林線是格林函式的等位面的正交軌線。

設區域D的格林函式為G(x,a)，a為D中某個取定的點，那么它的正交軌線稱為格林線。

性質

對a的充分小鄰域內的每一點x₀(x₀≠a)，有惟一的格林線經過它，這種格林線惟一對應著從a處出發與該格林線相切的射線，這種對應給出了從a點發出的格林線全體與射線全體之間的一一映射，其中從a發出的格林線，若在其上滿足inf G=0，則此格林線稱為正則的。因此，從a發出的格林線幾乎都是正則的，即其中非正則者所對應的射線與球面S(a,C)={x||x-a|=C}的交是(n-1)維的勒貝格零測集。

此外，存在一個n維勒貝格零測集N，包含了臨界點全體N，使在每一點x₁∈D\N有惟一的正則格林線Γ經過。

推廣

讓x₁與r=G(x₁,a)及Γ在a的單位切向量l組成的有序對(r,l)建立對應，就得到D\N中的格林坐標系，(r,l)稱為x₁的格林坐標。它是研究格林區域上的位勢的重要工具。

若用s表示Γ從a到x₁處的弧長，那么有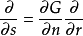在D\N成立，此處∂G/∂n表示等位面在x₁處的外法嚮導數。