基本介紹
- 中文名:柱
- 外文名:column
分類
按截面形式分
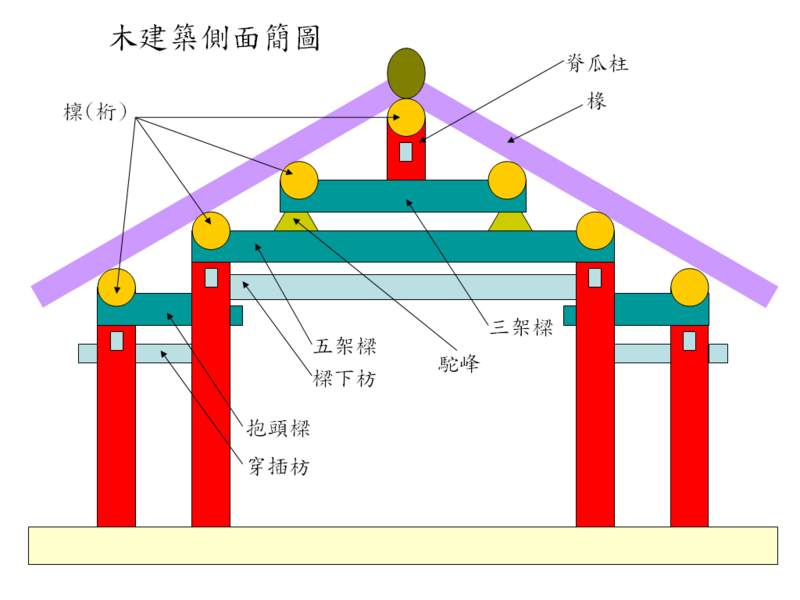 木建築側面簡圖
木建築側面簡圖按所用材料分
按長細比分為
 柱的其中之一
柱的其中之一柱體失穩

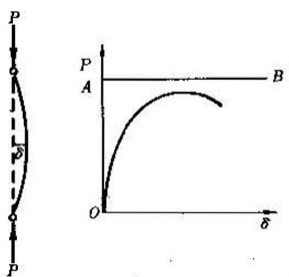
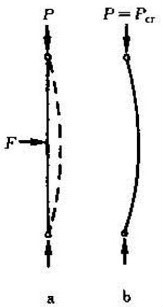 圖1 受壓柱的兩種平衡狀態
圖1 受壓柱的兩種平衡狀態細長柱的線彈性失穩
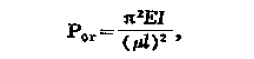




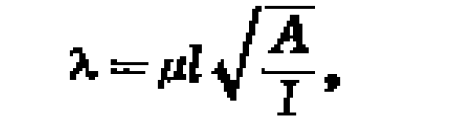
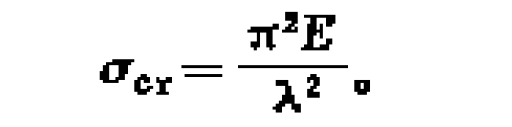

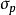
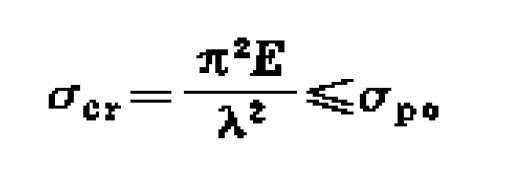
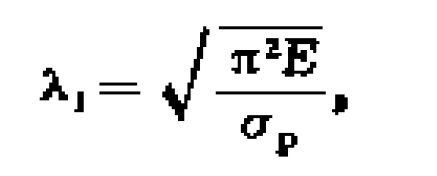
中長柱的非線彈性失穩

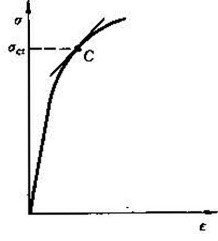
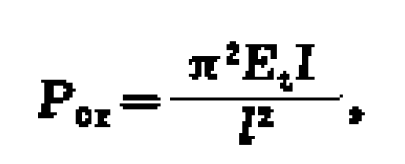
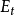


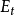
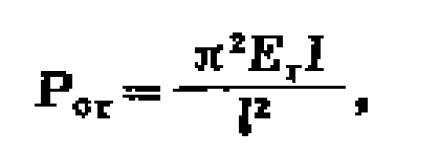
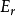
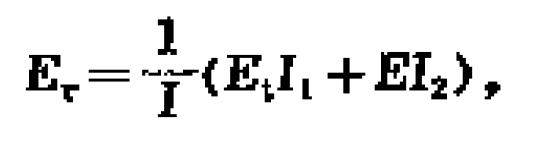
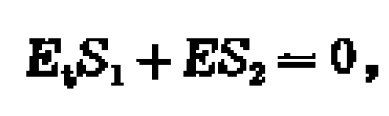
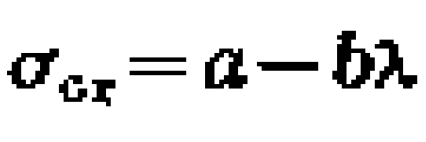

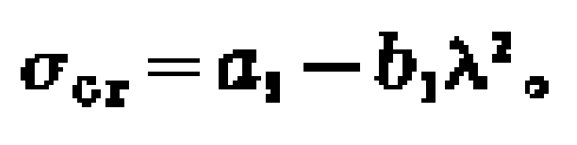
短柱的強度破壞


 木建築側面簡圖
木建築側面簡圖 柱的其中之一
柱的其中之一
 圖1 受壓柱的兩種平衡狀態
圖1 受壓柱的兩種平衡狀態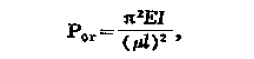




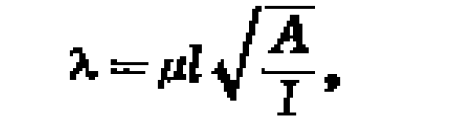
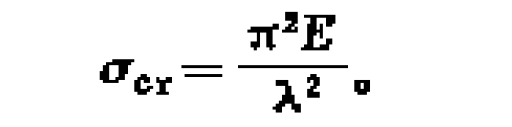

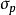
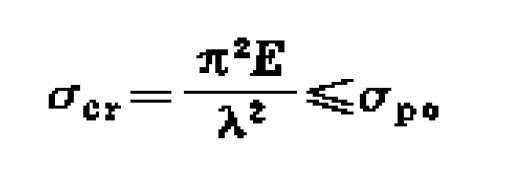
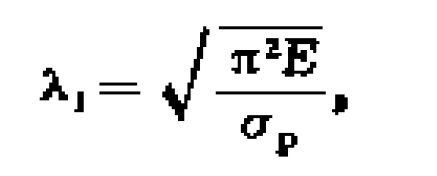


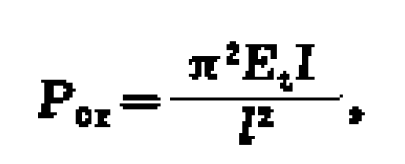
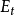


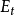
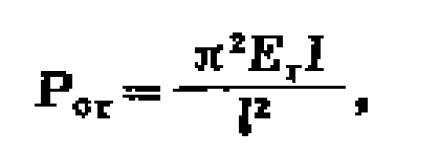
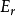
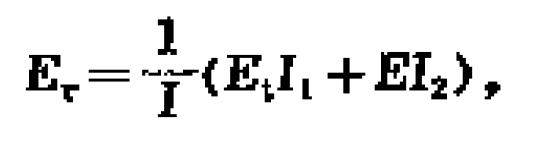
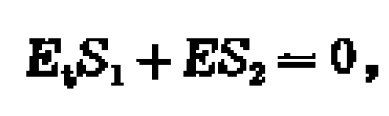
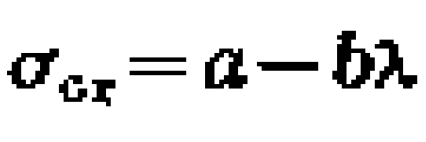

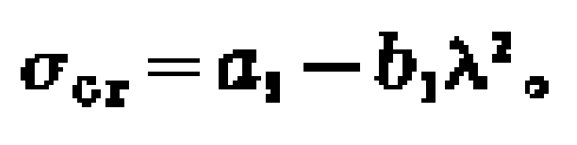



柱是建築物中垂直的主結構件,承托在它上方物件的重量。在中國建築中,橫樑直柱,柱陣列負責承托梁架結構及其他部分的重量,如屋檐,在主柱與地基間,常建有柱礎。...
分類:柱按截面形式分為方柱、圓柱、管柱、矩形柱、工字形柱、H形柱、T形柱、 L形柱、十字形柱、雙肢柱、格構柱;按所用材料分為石柱、磚柱、砌塊柱、木...
常說的過柱應該叫柱層析分離,也叫柱色譜。我們常用的是以矽膠或氧化鋁作固定相的吸附柱。由於柱分的經驗成分太多,所以下面我就幾年來過柱的體會寫些心得,希望能...
在建築物縱中線上,除山面二端外,頂端支承脊槫(桁、檁) 的通柱稱為中柱。中柱柱徑較其他各柱為大。宋式建築又稱分心柱。...
柱之男, 日本漫畫《JOJO的奇妙冒險》第二部中出現的超級生命,超越人類的遠古生命體。...
“人柱力”是在日本漫畫火影忍者(NARUTO)中出現的名詞“じんちゅうりき”的當用漢字。所謂人柱力,即被尾獸或者尾獸查克拉附身的人,作為封印尾獸或其查克拉的容器...
柱礎是中國建築構件一種,俗稱磉盤,或柱礎石,它是承受屋柱壓力的墊基石,凡是木架結構的房屋,可謂柱柱皆有,缺一不可。古代中國人民為使落地屋柱不使潮濕腐爛,在...
柱一(ε Aur/ 御夫座ε) 是在御夫座的一顆恆星,它的固有名稱是Haldus、Almaaz、或Al Anz。視星等3.04。以9,890天(大約27.1年)的周期在+3.0和 +3.8等...
西魏時期受封的八位柱國大將軍,史稱“八柱國”,分別為:宇文泰,元欣,李虎(李淵祖父),李弼(李密曾祖父),趙貴,于謹,獨孤信(宇文毓和楊堅岳父,李淵的外祖父)...
色譜柱由柱管、壓帽、卡套(密封環)、篩板(濾片)、接頭、螺絲等組成。...... 色譜柱由柱管、壓帽、卡套(密封環)、篩板(濾片)、接頭、螺絲等組成。...
一柱,漢語辭彙,三種意思:一根柱子;喻能擔當重任,獨力支撐局面的人;指舊式賬簿或清冊里的一個項目。...
框架柱就是在框架結構中承受梁和板傳來的荷載,並將荷載傳給基礎,是主要的豎向支撐結構。...
中柱(維管柱)是指內皮層以內的中軸部分。中柱包括中柱鞘,它位於中柱外圍與內皮層相毗鄰,常由一至幾層連續的薄壁細胞構成;部分維管形成層、木栓形成層、側根...
柱坐標系是指使用平面極坐標和Z方向距離來定義物體的空間坐標的坐標系稱,如空間直角坐標系相同,柱坐標系中會有一個值變數。...
問:申城的高架立柱中,有一條“九龍柱”赫赫有名,說的就是延安路高架和南北高架交叉處的那根立柱。和其他柱子不同的是,這根立柱特別粗壯,柱子通身包裹不鏽鋼和...
鹽柱位於阿茲多瑪,出自《聖經·創世記》。...... 鹽柱簡介 編輯 在死海的南端,有一座名叫阿茲多瑪Usdom的小山,也就是所多瑪城之名,此地有許多硫磺涌流出來,山...
柱色譜法,又稱層析法。是一種以分配平衡為機理的分配方法。色譜體系包含兩個相,一個是固定相,一個是流動相。當兩相相對運動時,反覆多次地利用混合物中所含各組...
氣柱袋又稱緩衝氣柱袋、充氣袋、氣泡柱袋、柱狀充氣袋,是21世紀使用自然空氣填充的新式包裝材料。...
羅馬柱,它的基本單位由柱和檐構成。柱可分為柱礎、柱身、柱頭(柱帽)三部分。由於各部分尺寸、比例、形狀的不同,加上柱身處理和裝飾花紋的各異,而形成各不相...
柱式是指一整套古典建築立面形式生成的原則。基本原理就是以柱徑為一個單位,按照一定的比例原則,計算出包括柱座(Base)、柱身(shaft)和柱頭(Capital)的整個柱子的...
砼柱是漢語辭彙,拼音是tóng zhù,意思是混凝土柱子。...... 砼柱是漢語辭彙,拼音是tóng zhù,意思是混凝土柱子。中文名 砼柱 外文名 Concrete column 拼音 ton...
柱後是一個漢語詞語,讀音是zhù hòu,是指執法官、御史等所戴的一種帽子。...... 柱後是一個漢語詞語,讀音是zhù hòu,是指執法官、御史等所戴的一種帽子。...
柱石,漢語辭彙。拼音:zhù shí釋義:1、頂梁的柱子和墊柱的礎石。2、擔當重任的人。3、擔當重任...
尾生抱柱是一個漢語成語,讀音是wěi shēng bào zhù,意思是相傳尾生與女子約定在橋樑相會,久候女子不到,水漲,乃抱橋柱而死。一般用以比喻堅守信約。出自《...
構造柱是指為了增強建築物的整體性和穩定性, 多層磚混結構建築的牆體中還應設定鋼筋混凝土構造柱,並與各層圈樑相連線,形成能夠抗彎抗剪的空間框架,它是防止房屋...
