柯西色散公式(Cauchy's dispersion formula)是指的是法國數學家柯西發現媒質的折射率與真空中入射光的波長的關係。該公式是n(λ)=a+b/λ2+c/λ4。
基本介紹
- 中文名:柯西色散公式
- 外文名:Cauchy's dispersion formula
- 公式:n(λ)=a+b/λ^2+c/λ^4
- 類型:色散公式
- 領域:光學
簡介,理論推導,
簡介
n(λ)=a+b/λ2+c/λ4。
其中 a,b,c 是三個柯西色散係數,因不同的介質而不同。
只須測定同一物質的三個不同的波長下的折射率n(λ),代入柯西色散公式中可得到三個聯立方程式,解這組聯立方程式就可以得到該介質的三個柯西色散係數。有了三個柯西色散係數,就可以計算出其他波長下的折射率不需要再測量。
除了柯西色散公式之外,還有其他的色散公式。如 Hartmann色散公式、Conrady色散公式、Hetzberger色散公式等。 不同頻率的光對同一介質的折射率並不相同。
不同頻率的光對同一介質的折射率並不相同。
 不同頻率的光對同一介質的折射率並不相同。
不同頻率的光對同一介質的折射率並不相同。理論推導
我們不妨假設有一列平面波(也就是一束平行光)沿著 z 軸照射到介質表面,平面波的方程為

假設這列光波要通過一個厚度為 Δz 的介質,如果在介質中光速為c/n,那么在介質中光就會額外花費一些時間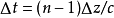 來傳播。
來傳播。
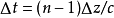
於是,在介質之後的光矢量就是

於是,在介質之後的光矢量,與原先的光矢量相比,相當於“延後”了一個相位。也就是乘以了一個相位因子 。
。

當光從真空中照射到一種介質(比如玻璃)上,這種介質分子內部的帶電粒子,就會受到影響而振盪起來。當然原子核受到各種約束其實是振盪不起來的,振盪起來的只是原子外層的電子。
如果我們設定介質表面位於 z=0 的地方,那么介質表面處的光矢量就是

那么在介質中的電子就受到這樣一個回復力進行運動。如果我們認為原子外層的電子,其運動行為類似於一個彈簧振子(這個假設非常地想當然,但的確是對真實情況的一種很好的近似),那么一個彈簧振子在周期性回復力下表現為一個簡諧振動,運動方程為

所有電子都在其平衡位置附近做這樣的簡諧振動。所有電子同時做這樣的簡諧振動,就產生了一個整體的振動的場強,從而產生了一個新的光矢量

對比一下,可以知道

其中,


把上面式子裡無關的常數都放到一起,頻率換成波長,可以得到這樣的結果:

這裡,


對於常見的玻璃來說, 在紫外區域。對於可見光波長範圍內的
在紫外區域。對於可見光波長範圍內的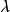 都有
都有 。按照級數展開,就有
。按照級數展開,就有

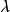


由此可見,儘管柯西色散公式是一個經驗公式,但確實能夠從折射率的微觀機理上得到解釋。
事實上,透明材料(比如玻璃)往往具有多個不同的固有頻率,同時電子的受迫振動也並非簡諧振動而是阻尼振動。將這兩項因素考慮進上面的推導過程,能得出更接近實際情況的折射率表達式。但對於推導柯西色散公式來說,這裡就足夠了。



