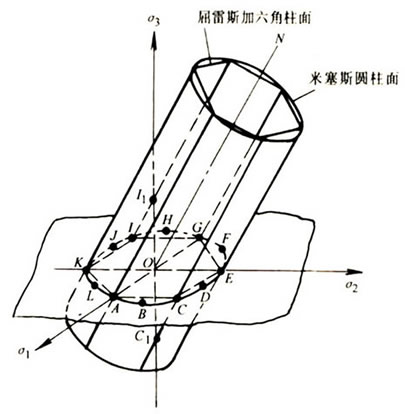
基本介紹
- 中文名:松崗元-中井屈服準則
- 外文名:Matsuoka yuan - in the well yield criterion
- 表現形式:屈服面或屈服位置
- 作用:解塑性成形問題必要的補充方程
- 屬於:屈服準則
- 學科:物理學
條件,舉例,各向同性屈服準則,各向異性屈服準則,
條件
A.受力物體內質點處於單向應力狀態時,只要單向應力大到材料的屈服點時,則該質點開始由彈性狀態進入塑性狀態,即處於屈服。
B.受力物體內質點處於多向應力狀態時,必須同時考慮所有的應力分量。在一定的變形條件(變形溫度、變形速度等)下,只有當各應力分量之間符合一定關係時,質點才開始進入塑性狀態,這種關係稱為屈服準則,也稱塑性條件。它是描述受力物體中不同應力狀態下的質點進入塑性狀態並使塑性變形繼續進行所必須遵守的力學條件,這種力學條件一般可表示為
f(σij)=C
又稱為屈服函式,式中C是與材料性質有關而與應力狀態無關的常數,可通過試驗求得。
屈服準則是求解塑性成形問題必要的補充方程。
舉例
以下代表套用於各向同性材料的最常見的屈服準則(在所有方向上均勻的性質),其他方程式已經被提出或套用於某種專業情況下。
各向同性屈服準則
最大主應力理論
該理論由W.J.M Rankine於1850年提出,該理論認為當最大主應力超過單軸拉伸屈服強度時,產生屈服。 雖然這個標準允許與實驗數據進行快速的比較,但很少適用於設計目的。 但是,這個理論給出了脆性材料的良好預測。
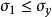
最大主應變理論
該理論由St.Venant提出,該理論認為當在簡單拉伸試驗期間最大主應變達到對應於屈服點的應變時,產生屈服。 在主應力方面,這取決於方程:
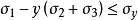
最大剪下應力理論
該理論由法國科學家亨利·特雷斯卡提出,後也被稱為特雷斯卡屈服準則。 該理論假設當剪下應力超過剪下屈服強度,產生屈服。
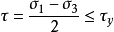
總應變能量理論
該理論假設與屈服點處的彈性變形相關的儲存能量與特定應力張量無關。 因此,當單位體積的應變能量大於在簡單張力下的彈性極限處的應變能時,產生屈服。由此給出, 對於三維應力狀態:
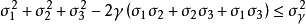
最大失真能量理論
該理論提出,總應變能可以分為兩部分:體積(靜水力)應變能和形狀(變形或剪下)應變能。 當簡單拉伸試驗時,當變形分量超過屈服點時,產生屈服。 這個理論也被稱為von Mises的收益標準。
基於不同的理論基礎,該表達也被稱為八面體剪下應力理論。
其他常用的各向同性產量理論包括:
von Mises收益標準
Drucker-Prager產量理論
Bresler-Pister產量理論
Willam-Warnke收益理論
各向異性屈服準則
當金屬受到大的塑性變形時,晶粒尺寸和取向在變形方向上變化。 由此,材料的塑性屈服行為表現出方向依賴性。 在這種情況下,諸如von Mises收益率標準的各向同性收益率標準無法準確地預測收益行為。 這時,就需要幾種各向異性屈服準則來處理這種情況。[2]一些更普遍的各向異性產率理論包括:
希爾的二次收益理論
廣義山產量理論
霍斯福德產量理論。