李特爾伍德-佩利理論是指關於lp(p>1)空間中傅立葉級數的理論,1931~1940年由J.E.李特爾伍德、R.E.A.C.佩利首創,後由A.贊格蒙、J.馬欽凱維奇等加以發展。
基本介紹
- 中文名:李特爾伍德-佩利理論
- 提出者:J.E.李特爾伍德、R.E.A.C.佩利
- 提出時間:1931~1940年
- 套用學科:數學

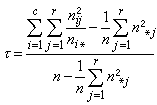
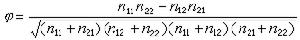
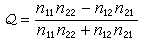
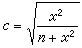
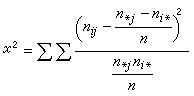
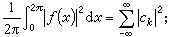
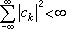
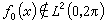
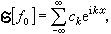
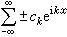
李特爾伍德-佩利理論是指關於lp(p>1)空間中傅立葉級數的理論,1931~1940年由J.E.李特爾伍德、R.E.A.C.佩利首創,後由A.贊格蒙、J.馬欽凱維奇等加以發展。

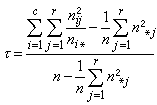
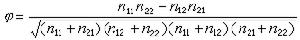
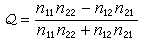
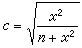
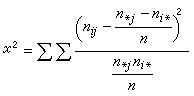
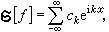
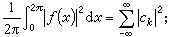
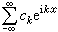
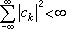
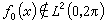
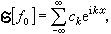
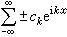
李特爾伍德-佩利理論是指關於lp(p>1)空間中傅立葉級數的理論,1931~1940年由J.E.李特爾伍德、R.E.A.C.佩利首創,後由A.贊格蒙、J.馬欽凱維奇等加以發展。關於(>1)空間中傅立葉級數的理...
從1931年開始,他同R.E.A.C.佩利合作,研究傅立葉級數與冪級數,建立了以他們的名字命名的李特爾伍德-佩利理論。這一理論在近代調和分析中占有重要的地位,並且仍在繼續發展中。哈代-李特爾伍德極大函式,也經常被引用。出版著作 李特爾...
李特爾伍德-佩利g函式的基本性質是:若1 Lp空間 在數學中, L空間是由p次可積函式組成的空間;對應的l空間是由p次可和序列組成的空間。在泛函分析和拓撲向量空間中,他們構成了Banach空間一類重要的例子。L空間都是巴拿赫空間,但只有...
李特爾伍德-佩利理論 上述豪斯多夫-楊定理的實質,是用傅立葉係數的大小來反映函式所屬的空間,但它並沒有給出空間L(0,2π)的傅立葉級數特徵。因此,不可能象帕舍伐爾公式那樣,用傅立葉係數的大小來刻畫l(0,2π)中函式的特徵。
是Fₖuₖ的李特爾伍德-佩利二進分解;對應的環體是 ,2N是 中與 相交的環體的個數。性質 F在仿微分運算元理論中有許多與傅立葉積分運算元在擬微分運算元理論中相似的性質。特別地,也有葉戈羅夫相似性定理。於是就有可能對仿微分運算元...
此外,在研究微分運算元的有界性時,傅立葉譜分析方法有時並不有效,此時人們常常用到李特爾伍德-佩利分解,而這種分解在餘切從上有十分好的幾何特徵。近年來,微局部分析方法還被進一步發展而用於處理各類非線性問題。
