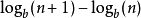基本介紹
- 中文名:本福特定律
- 外文名:Benford's law
- 別名:本福德法則
- 發現時間:1938年
定義,數學,不完整的解釋,套用,歷史,參見,
定義
本福特定律,也稱為本福德法則,說明一堆從實際生活得出的數據中,以1為首位數字的數的出現機率約為總數的三成,接近期望值1/9的3倍。推廣來說,越大的數,以它為首幾位的數出現的機率就越低。它可用於檢查各種數據是否有造假。
數學
在十進制首位數字的出現機率(%,小數點後一個位):
| d | p |
|---|---|
1 | 30.1% |
2 | 17.6% |
3 | 12.5% |
4 | 9.7% |
5 | 7.9% |
6 | 6.7% |
7 | 5.8% |
8 | 5.1% |
9 | 4.6% |
不完整的解釋
一組平均增長的數據開始時,增長得較慢,由最初的數字a增長到另一個數字 a+1起首的數的時間,必然比a+1起首的數增長到a+2,需要更多時間,所以出現率就更高了。
從數數目來說,順序從1開始數,1,2,3,...,9,從這點終結的話,所有數起首的機會似乎相同,但9之後的兩位數10至19,以1起首的數又大大拋離了其他數了。而下一堆9起首的數出現之前,必然會經過一堆以2,3,4,...,8起首的數。若果這樣數法有個終結點,以1起首的數的出現率一般都比9大。
這個定律的嚴格證明,可以參見Hill, T. P. "A Statistical Derivation of the Significant-Digit Law." Stat. Sci. 10, 354-363, 1996.。
套用
1972年,Hal Varian提出這個定律來用作檢查支持某些公總計劃的經濟數據有否欺瞞之處。1992年,Mark J. Nigrini便在其博士論文"The Detection of Income Tax Evasion Through an Analysis of Digital Frequencies."(Ph.D. thesis. Cincinnati, OH: University of Cincinnati, 1992.)提出以它檢查是否有偽帳。
推而廣之,它能用於在會計、金融甚至選舉中出現的數據。該定律被華盛頓郵報上的一篇文章引用,該文章以此為基礎聲稱2009年伊朗總統大選中有造假[1]。