有線接入網成本模型

通過建立統一的“有線接入網成本模型”，量化描述各種建設場景下，接入網建設成本與具體建設環境（如機房、管線、用戶密度等）因素間的相互關係，並在此基礎上，計算出最佳覆蓋半徑，為多方案間成本比選及成本最佳化提供決策依據。

基本介紹

• 中文名：有線接入網成本模型
• 套用學科：通信

目的和任務

接入網建設是一個對業務、技術、成本十分敏感的領域，投資大、建設周期長，技術經濟風險控制困難。同時，接入網建設環境又十分複雜，同樣的用戶需求往往可以採取多種不同的接入方案，而各種建設場景的具體條件和用戶發展的不確定性給多方案比選帶來了極大的困難，這些因素使得當前的接入網建設帶有一定的盲目性，投資風險也進一步加大。

通信網理論認為：接入網為一定面積內的一定數量用戶提供接入服務，其網路總投資具有以下特點。

① 總投資主要由四部分構成：局端設備、機房與配套、管道與線路、用戶終端。

② 局端設備和用戶端設備總投資只與用戶數N和設備單價有關，當用戶數和設備單價一定時，可按常數處理。

③ 機房投資與管線投資成反比：機房數量越多，用於機房建設的投資越大，單個機房平均覆蓋半徑越小，平均每用戶線長度越短，則管線投資就越小。反之亦然。

因此，四部分投資變化的趨勢如圖2.1所示，接入網總投資存在理論上的最小值。

圖2.1 接入網總投資特點

有線接入網成本模型

2.2.1 覆蓋方式及平均每用戶線纜長度

（1）基本假設

基本假設：存在任意有限大區域D（D為該區域的接入半徑，定義為其幾何中心至區域邊界的最遠距離），區域中目標用戶數為N，且該區域內用戶呈均勻分布，密度為r。欲在該區域內新建有線接入網，覆蓋區域內全部用戶。建設方案為：將該區域劃分為多個接入區，每個接入區的接入距離為d（d代表區域中心到區域邊緣的最遠接入距離）。

（2）覆蓋方式選擇

針對任一有限區域，採用多局制覆蓋，考慮三種典型的覆蓋方式：圓形覆蓋、正六邊形覆蓋和正方形覆蓋，如圖2.2所示：

圖2.2 覆蓋方式圖示

對比上述三個接入覆蓋模型，模型一採用圓形覆蓋，效率最高但無法實現無縫覆蓋，不具備現實網路可操作性；模型二採用正六邊形覆蓋，主要適用於無線接入網套用環境；現實的有線接入網中，由於受到道路和街區劃分的影響，大多數接入區呈近似正方形，因此，有線接入網成本模型選取模型三作為主要研究對象。

（3）平均每用戶線纜長度

現實接入網路中，兩點間的用戶線纜很少以直線相連。絕大多數情況下，接入管線將沿街道採取折線方式到達用戶端。因此，引入直折比係數k₀，用戶接入線纜長度（L）=用戶接入距離（d）/直折比係數（k₀）。

參考圖2.3，有：

經計算：當覆蓋區域為正方形時，k₁=0.54（詳見附錄1）；現實網路中，k₀取值一般為0.6～0.8（詳見附錄2）。

註：不同的覆蓋模型對應不同的覆蓋效率係數：經計算，模型一（圓形覆蓋）對應的k₁=0.67；模型二（正六邊形覆蓋）對應的k₁=0.6（詳見附錄1）。

圖2.3 平均每用戶線纜長度計算模型

2.2.2 接入網投資結構及成本模型

總體上講，接入網投資結構主要包括四大部分：接入線纜投資、接入機房投資、局端設備投資、用戶側投資。

1．接入銅纜（光纜）投資（C₁）

該部分投資與用戶總數 、用戶平均線纜長度 、用戶線纜平均單價 （已包含管道投資分攤， 的引入代表了線路中存在分光器的情況）成正比：

如圖2.4所示，實際的有線接入網往往由主幹、配線、引入線三層組成。一般來講，主幹線纜距離較長、數量較少、但每根線纜芯數很大；配線線纜距離較短、數量較多、但每根線纜芯數較小；引入線最靠近用戶，線纜數量最多，相應的線纜芯數也最小。在成本方面，線纜芯數越大，往往每對芯線的製造成本就較低，且線纜的綜合成本包含了管道建設成本及相應敷設工程費用的分攤，芯數越大分攤到每對芯線上的其他費用也越低，因此，主幹線纜的單位造價最低，配線部分次之，引入線則較高。一般來講，從用戶引入線角度考慮，應該為所有潛在用戶提供接入能力。但在實際網路中，不可能所有的潛在用戶都成為某運營商的實裝用戶。在網路部署中，為了提高資源利用效率，節省投資，往往會設定一定的配線比進行線對數的收斂。當前銅纜接入網主配比一般設定為1∶1.2。在未來充分競爭條件下，運營所占市場份額趨於均衡，為了提高主幹線對利用率，還應進一步提高配線比，可考慮1∶1.2～1∶1.6。

圖2.4 接入網纜線分配示意圖

在上述因素的綜合作用下，接入纜線綜合成本經分攤後得到的用戶線纜平均單價實際上是一個分段函式，表示如下：

其中： 為分光比， 表示連線埠收斂比，也可以看作多用戶ONU所帶用戶數。對於傳統銅纜接入網， 。

理想情況下，正方形OLT覆蓋內的主幹節點覆蓋區及配線節點覆蓋區都應採用正方形覆蓋方式，應該滿足：,

且主幹、配線及引入線長度均與覆蓋區線纜總長度正相關，有：

則用戶線纜平均單價

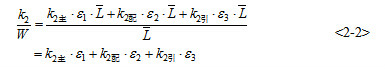
2．接入機房投資（C₂）

接入機房投資與機房數量和機房單價k₃相關： 。

說明：k₃代表的是與接入網路中節點數據成正比的那部分投資，主要由土建投資、傳輸設備投資、電源設備、地線及其他配套投資組成。

局端接入設備投資 ；用戶側投資 （其中：k₄為單位用戶接入設備成本；c為用戶側單位成本。c₃和c₄與接入半徑無關）。

綜合上述，有：

參數說明：

C：有線接入網總投資

C₁：接入線纜投資

C₂：接入機房投資

C₃：局端設備投資

C₄：用戶側投資

k₀：直折比

k₁：覆蓋形狀係數

：線路單價

k₃：機房單價（含配套）

k₄：接入設備單價

c：用啟側單位投資

式<2-3>對d求導並考慮到 ，可求得當接入距離（覆蓋半徑）滿足下式<2-4>時

接入網總投資有最小值：

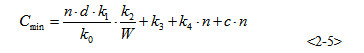
注意：n表示接入距離為 的覆蓋區域內的用戶數量，且有 ，則可求得接入網每用戶最小投資 ：

式<2-6>以最佳接入半徑為假設條件，在現實網路中，接入端局一旦建成，其覆蓋半徑是固定的，無法隨用戶密度的增加而增加，此時，令d取常數得到式<2-7>

現實網路中，取 時 ，

每用戶投資：

說明：參數“I”的計算將整體網路投資平均分攤到所有目標用戶頭上，是一種接入網建設的理想情況（可將“I”稱為網路覆蓋成本）。實際網路運營中，實裝用戶數必定只是網路目標覆蓋用戶數的一部份，且實裝用戶數N_實滿足：

但是，在網路運營過程中，網路實裝用戶數N_實不僅受式<2-9>的限制，更主要的是與運營商市場銷售及業務運營水平相關。相比之下，可以認為網路覆蓋成本“I”能夠更好地反映網路建設水平且受其他因素（如銷售、運維等）的影響較小。因此，本書將以網路覆蓋成本作為控制接入網建設成本的主要指標。在接入網建設實施後，如何使網路實裝用戶數接近或達到覆蓋用戶數，則是運營商行銷與服務戰略應考慮的目標。

例1 對一個有限大新建區域，採用傳統銅纜方式建設接入網，按2008年的建設市場價格及相關工程經驗，取定相關參數如下：

k₀=0.65；

k₁=0.54；

k₂=280元/線對·公里（含管道）；

k₃=300000元（城區，含配套）；

k₄=260元（寬頻）+220元（窄帶）（表示用戶同時有寬窄帶需求）

r=3000戶/平方公里；

c=50米/戶´0.64元/米+125元=157元/戶（表示每戶平均引入線投資32元，Modem為125元）

w₁=w₂=1。

則按式<2-4>可計算該區域最佳覆蓋半徑如下：

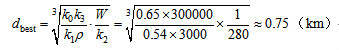
此時，按<2-5>式計算對應的每用戶最小投資為：

在實際網路中，城區銅纜覆蓋半徑一般為2～3km（按2.5km取值），則與2.5km覆蓋半徑對應的每用戶投資可按式<2-8>計算如下：

說明：

① 本例中的計算結果是在假定銅纜接入網主幹、配線單價相同、配線比為1∶1、用戶同時配置寬頻和窄帶板卡的情況下的網路覆蓋成本。

② 機房單價構成：購置成本20萬元（平均按40平方米´0.5萬元考慮），傳輸3萬元/套，配套部分7萬元（地線0.4萬元、裝修2萬元、外電引入0.3萬元、開關電源2萬元、電池1萬元、走道及其他），小計30萬元。

從上述計算可以看出：傳統銅纜接入網主要提供窄帶語音接入，由於歷史原因，在當前價格體系下，其覆蓋半徑已經偏大，造成平均每用戶銅纜接入成本偏高。

2.2.3 接入網投資關鍵因素分析

1．用戶密度與最佳覆蓋半徑的關係

在最佳半徑公式 中，最佳覆蓋半徑與直折比k₀、機房造價k₃成正比，與覆蓋效率k₁、用戶密度 和線路單價 成反比。

參考例1，在密集城區採用傳統銅纜組網時，接入網最佳覆蓋半徑與用戶密度的關係如圖2.5所示。

圖2.5 用戶密度與最佳接入半徑的關係

2．接入半徑對總投資的影響

考察式<2-8>，當實際網路覆蓋半徑與理論最佳覆蓋半徑發生偏離時（令 ），實際用於網路上的投資（即管線+機房投資）符合下式（此時，局端設備投資 和用戶側投資 與覆蓋半徑無關）：

每用戶網路投資：

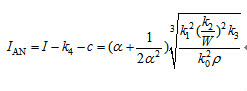
在此，主要考察變數間的相對關係，不妨設

則不同覆蓋半徑與平均每用戶網路投資相對關係如圖2.6所示。

① 當實際覆蓋半徑偏離理論最佳半徑時，接入網整體投資上升。

② 對最佳半徑偏離相同比例時（如擴大50%和縮小50%），擴大覆蓋半徑造成的成本上升小於相對應的縮小相同比例半徑造成的成本上升。函式分析表明，擴大覆蓋半徑，成本上升主要受線型函式 的影響；縮小覆蓋半徑，成本上升主要受非線性函式 的影響。

推論：在現實的網路實施中，很難按照理論絕對準確地計算控制局所覆蓋半徑。考慮到適當擴大半徑有利於減少機房數量並降低維護成本，同時建網成本上升相對平緩，因此建議在實際組網時，可根據現場環境適當擴大局所覆蓋範圍。同理，對縮小局所覆蓋範圍，設定更多接入局所要慎重考慮—該操作有可能引起接入成本迅速上升並給後期網路維護工作造成困難。

圖2.6 覆蓋半徑偏離對接入網路投資的影響

3．對平均密度假設的分析

前文基於平均密度假設建立了成本模型，即假定在某一有限區域的用戶分布是連續且均勻的。但是，在現實環境中（參見圖2.7），各個街區被道路所分割。街區內分布有小區、大樓、廠房、公園、綠地，從微觀上看，用戶的分布也不連續，局部用戶密度更是差異巨大（如摩天大樓與旁邊的綠地、公園）。

圖2.7 城市布局實例

此時，若需對某一現實場景進行有線接入網規劃，則在用戶密度的計算上需要對如下兩種“近似”方案進行選擇。

巨觀區域選擇（方案一）：按較大尺度（1km以上）進行用戶平均密度的計算，即假定在巨觀尺度內部，用戶分布是均勻連續分布的。

微觀區域選擇（方案二）：考慮微觀尺度，按小區甚至大樓等局部密度進行計算。

上述兩種方案都可以進行有線接入網規劃，但方案一更具可操作性且能節省投資，理由如下。

1. 接入網規劃要求對目標區域進行整體無縫覆蓋，方案二從微觀入手，按小區甚至大樓的局部密度進行規劃，這種面向點狀目標的規劃方法很難體現面覆蓋的概念。

2. 用方案二規劃方法實現無縫覆蓋時，網路上將出現大量小半徑接入區，且眾多接入區覆蓋半徑相互重疊，意味著各接入區實際覆蓋半徑將明顯小於理論最佳值。參照圖2.6曲線可知，此時接入成本上升服從平方反比關係，將造成接入網總體成本大幅上升。

3. 採用方案二指導網路建設，將造成網路上出現數量巨大的有源接入節點，與網路扁平化、簡化網路結構、節省維護成本，降低網路故障率的目標背道而馳。

因此，實際網路規劃應採用巨觀區域選擇方式進行用戶密度計算。

關於模型可用性的說明

接入網建設受成本因素影響極大，在這裡嘗試採用統一的接入網成本模型量化計算接入網組網成本。該部分計算在數學模型指導的基礎上，藉助大量工程經驗參數進行計算，得出了一些初步結論，作為接入網網路建設成本計算的參考。

但是，現實的網路建設實踐是十分複雜的，具體的網路建設受到諸多環境因素的制約，不可避免地與理想模型存在一定的偏差，對此，關於模型有如下幾點說明。

（1）目前世界範圍內有關接入網成本模型仍未形成系統的理論和體系。由於影響接入網成本的因素太多，很多因素糾纏在一起並受到現實場景的影響，目前的成本計算模型還做不到面面俱到。這就決定了處理同一個問題時必然會出現或引伸出多種方法——本章試圖通過理想的數學模型粗略地模擬出影響接入網建成本的主要因素及其量化關係，主要目的是為後續接入網規劃提供參考，不必要求它的精度很高。

（2）可以預見，基於理論分析的參數取值（如k₀，k₁等）計算所得的預測結果套用到某一特定工程實踐中時，發生偏差是必然的。然而問題的關鍵在於：如果針對同一場景下不同的接入網組網方案採用同一模型進行量化分析，則各種組網方案受到的誤差影回響該是趨同的，所以，可以認為，採用成本模型能夠對多種接入網整體解決方案進行成本比選，所得結論適用於指導實際的接入網規劃及設計工作。

（3）為了定量計算，以幫助理清接入網規劃原則和思路，書中部分採用了基於統計得到的工程經驗數值，直接用於接入網典型套用場景的量化計算。這些數值大多取自我國中西部省份2008年的光纖接入網工程經驗參數，其準確性能適用於某些具體的套用場景，不具備直接套用到所有地區的普遍適用性。同時，書中所列舉的參考數據和比例係數也應該隨著工程套用的時間、地點的變化進行調整和更新。

最後，在套用此介紹的方法設計光纖接入網解決方案時，應結合本地的實際套用環境對相關參數進行修正，以便得到更加符合本地特點的接入網解決方案。