基本介紹
- 中文名:有效編碼假設
- 外文名:valid encoding assumptions
- 提出者:霍雷斯·巴羅
- 提出時間:1961年
- 涉及領域:神經生物學、計算機科學和心理學
主要內容,有效編碼模型,研究意義,挑戰發展方向,
主要內容
在腦中,神經元通過傳遞一些電脈衝進行聯繫,這種電脈衝被稱作動作電位或者神經衝動。感覺神經科學的一個目標,就是解碼這些動作電位的意義,以便理解腦是如何表現和處理外部世界的信息。巴羅假設,感覺系統的動作電位形成了神經編碼用來有效地表達感覺信息。 巴羅所說的“有效”,指的是神經編碼會使得傳遞一個給定信號所需要的動作電位數量最少。這有點類似在網際網路上傳遞信息,可以使用不同的檔案格式來傳送同一張圖片。對於同一張圖片來說,使用不同的檔案格式會需要不同的比特數來達到同樣的解析度。這個模型認為,腦會使用適合表達生物生活的自然環境的視覺和聽覺信息的編碼。
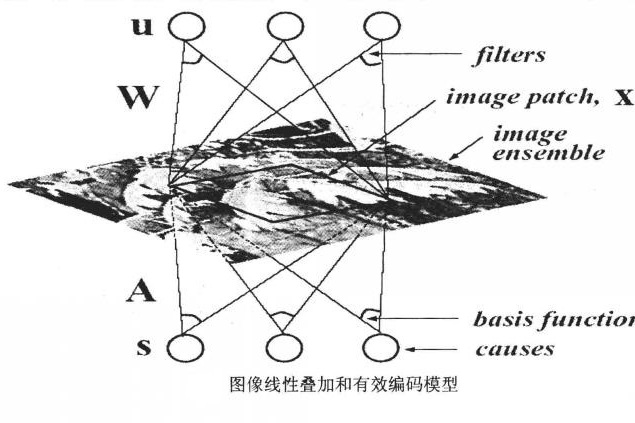
有效編碼模型
從方法論上,有效編碼研究主要可以分為兩條路線:直接的方法是從生物機理上,在自然圖像刺激條件下檢測神經細胞的回響特性,我們叫做機理測試;另外一個替代的方法是利用自然圖像的統計特性,建立模型模擬早期視覺處理系統的處理機制,叫做模型仿真。在有效編碼模型仿真中,我們首先考察外部環境刺激的統計特性,根據特定的統計最佳化準則建立回響模型,然後與初級視皮層中神經細胞的回響特性(神經生理學)進行比較。
隨著輸入信號維數的增加,描述輸入信號聯合分布的複雜度會指數增長。因此,我們通常針對特定的統計特性,或者指定特定的分解算法來簡化問題。常用的有效編碼算法可以分為三種。第一是基於二階統計量的線性有效編碼模型,第二是基於高階統計量的線性模型,第三是基於高階統計量的非線性模型。
研究意義
有效編碼理論是神經生物學、計算機科學和心理學的交叉研究領域。隨著對生物視覺系統研究的進一步細緻,以及計算機技術的飛速發展,近年來,有效編碼假設理論成為了人們研究的一個熱點,人們從神經生物學機理模型和計算機科學可計算模型等角度進行了廣泛的研究,很多重大的成果對生物和機器視覺,乃至腦科學的發展產生了重要的影響。
挑戰發展方向
儘管有效編碼假設無論從神經生物學機理還是從可計算模型都得到了廣泛的驗證,但是有效編碼假設在有些方面也不夠完善,受到部分研究者的質疑。以下是有效編碼假設理論的不足和挑戰,以及進一步研究的發展方向。
視覺目標
有效編碼的首要的不足就是沒有考慮視覺系統的目標。有效編碼假設理論只表明外界信息必須有效表示,但是沒有考慮表示什麼樣的信息。很多研究者認為在視覺通道的低級階段(例如視網膜,V1區),因為編碼的信息要被高級階段不同的神經細胞適用於不同的場合,編碼外界信號時保存儘可能多的外界信息是有道理的。有效編碼模型成功的解釋了視網膜,V1簡單細胞的回響特性說明了這一點。
但是,視覺通道高級階段的神經細胞就不一定符合有效編碼假設。有效編碼假設並沒有考慮編碼的信息怎么被使用,而只考慮怎樣使得編碼的信息最大化。顯然,視覺任務與視覺系統的內部編碼是密切相關的,不同視覺任務的內部編碼可能會不一樣。例如,為了識別一個對象所進行的編碼跟存儲一個對象的編碼是不一樣的,前者的編碼更加側重內部編碼的可識別能力,而後者更加側重編碼的容量。
有效編碼假設中必須使用Bayesian規則綜合考慮外界環境的統計特性和視覺任務或者目標,建立與視覺任務相關的更加完善的有效編碼理論。
視皮層神經細胞的冗餘表示
基於視網膜神經節細胞數目和初級視皮層神經細胞數目的比較,有些研究者對有效編碼假設提出了相反的觀點:“參與感官信息處理的神經細胞數目,越往視覺通道的高層其數目也越大,因此大腦的神經編碼增加了信息的冗餘性”。這個觀點的前提條件是每一個神經細胞的編碼能力是相同的。但是對於這一個前提很多研究表明並不是這么一回事,如果不同的神經細胞編碼的方式和編碼能力允許不一樣的話,那么使用多個神經細胞編碼的信息就不一定比用少數的冗餘。這在神經生理學是一個開放的課題。