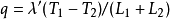工程套用意義
有效熱導率可用來概括其它更多、更複雜的因素。這種處理方法在工程近似計算中是有意義的,如下:
(1)把熱導率隨溫度而變化的物體視為熱導率為某一常值(有效熱導率)的物體;
(2)把幾種不同材料迭加而成的複合板視為某種均勻材料的板,以統一的有效熱導率去等效代替複合板內的不同熱導率,對各種工業爐牆常按此法處理;
(3)把在各向異性介質中沿某一方向進行的導熱過程視為是在各向同性介質中進行。在一定條件下用一個標量來描寫導熱能力,此標量即為有效熱導率;
(4)把含熱源的導熱區域視為無源的情形,修改原有熱導率而引入有效熱導率。對熱輻射既有吸收性又有穿透性的透明平板,有滲流的岩石等可視為屬此情形;
(5)把既有導熱又有對流兩種過程同時存在的區域人為地視為只有單純的導熱過程。用有效熱導率來表示導熱與對流同時作用的傳熱能力。在計算諸如鑄造等液態金屬凝固過程時,常用此種方法;
(6)把既有導熱又有傳質的綜合過程視為單純的導熱過程,用有效熱導率去等價地代替綜合的傳熱能力。潮濕土壤的熱導率、煉焦中煤的焦化過程都屬此列。
上述幾種有效導熱的情形可分兩大類:一類是,如(1)(2)(3),把複雜的材料予以理想化,把本不能用一定值去描述材料實際熱導率的問題人為地用有效熱導率代替。這種等效性是有條件的,不顧條件隨意推廣是不行的。另一類是,如(4)(5)(6)所 列,把本不是單純導熱現象人為地折合成某種導熱現象,且用有效熱導率去描述,在這裡,有效熱導率不僅與材料性能有關,還與過程特點有關。不顧過程的特點,隨意套用有效熱導率是不行的。
有效熱導率的計算
根據以上分析,有效熱導率的計算可分為以下幾種情況。
熱導率為常數的平板
(1)無熱源的情形
如圖,為無熱源平板,兩壁面溫度分別為T
1與T
2,熱導率為λ,板內溫度分布為:
,通過平板的熱流量q處處想等,且為:
。
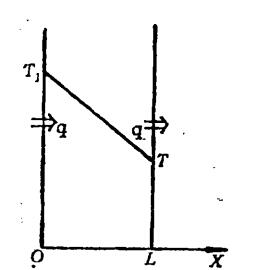 無內熱源平板內溫度的分布
無內熱源平板內溫度的分布(2)熱源強度為常數q''的情形
在x=L/2處,
;
 含內熱源平板內溫度的分布
含內熱源平板內溫度的分布當
時,板內只有沿單方向的熱流。此時計算q
0時可採用下式所示的有效熱導率λ':
;
顯然,λ'<λ,對應圖中比較平坦的一條虛線。在計算q
2時,有效熱導率為:
,對應圖中較陡的一條虛線。
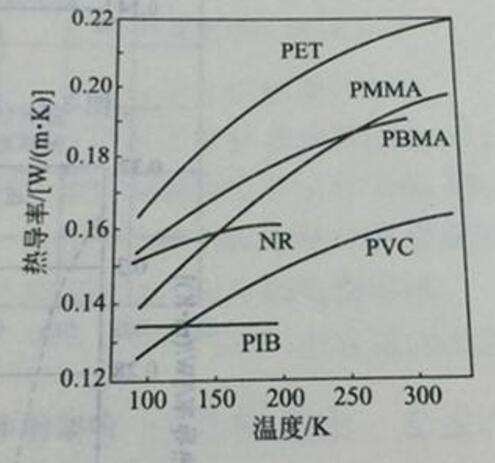
熱導率隨溫度變化的平板
在實際工程材料中,熱導率大都是溫度的函式,它隨溫度而變化的規律不盡相同。作為一階近似,假如它隨溫度的變化規律滿足下式,其中λ
0和a為常數:
。
(1)溫度變化的無熱源平板
在已知板的兩壁面溫度為T
1與T
2的條件下,板內溫度分布如圖所示,其函式形式為:
;
相應的熱流密度為
;
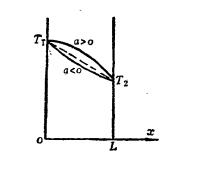 變物性平板內溫度分布
變物性平板內溫度分布由此計算得到有效熱導率λ'為
,λ
1和λ
2分別為T
1和T
2條件下的熱導率。
該結論也可用於圓筒壁與球壁的計算,只是在圓筒壁與球壁中不用熱流密度而用單位長度熱流量qt與總熱流量Q來代替。
(2)溫度變化的有熱源平板
對照無熱源平板公式,此時板內溫度分布滿足下列導熱微分方程:
;
在已知板的兩壁面溫度為T
1與T
2的條件下,板內溫度分布如圖所示,其函式形式為:
;
板內的熱流密度在不同x處是不同的,在x=0,x=L與x=L/2處的q
0、q
L與q
L/2與熱導率為常數的有熱源平板計算公式相同。
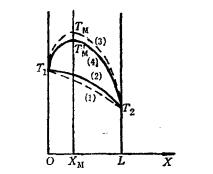 含內熱源變物性平板內溫度的分布
含內熱源變物性平板內溫度的分布雙層複合材料平板
(1)熱導率分別為常數λ1與λ2的情形
(2)熱導率分別為常數λ1=λ01+a1與λ2=λ01+a2的情形
由前面分析可知,當a1>0與a2<0時,板內的溫度分布曲線如圖所示,板內的熱流密度為:
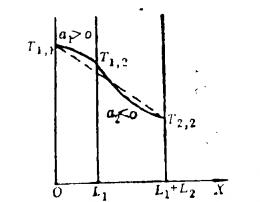 變溫度雙層複合平板內溫度分布
變溫度雙層複合平板內溫度分布其中λ1'、λ2'與λ'分別為:
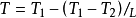
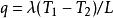
 無內熱源平板內溫度的分布
無內熱源平板內溫度的分布

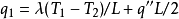
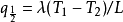
 含內熱源平板內溫度的分布
含內熱源平板內溫度的分布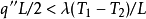

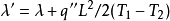


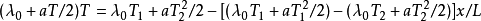
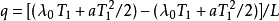
 變物性平板內溫度分布
變物性平板內溫度分布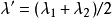

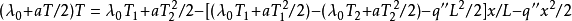
 含內熱源變物性平板內溫度的分布
含內熱源變物性平板內溫度的分布
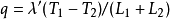

 變溫度雙層複合平板內溫度分布
變溫度雙層複合平板內溫度分布