有向三面角

有向三面角(directed trihedral angle)指確定了方向的三面角，即規定了三條棱的一種順序的三面角。三面角的三條棱有兩種不同的循環順序：有向三面角規定其中一種為正向，另一種為負向，從三面角的頂點向各棱所指的方向看，三條棱的兩種順序相當於順時針或逆時針方向，兩個有向三面角在三條棱的正面同為順時針(或同為逆時針)方向時稱為同向三面角，否則(即一為順時針方向另一為逆時針方向時)稱為反向三面角。

基本介紹

• 中文名：有向三面角
• 外文名：directed trihedral angle
• 所屬學科：數學
• 所屬問題：立體幾何（三面角）
• 簡介：確定了方向的三面角

定義

依次規定三面角的棱的繞向順序的三面角稱為有向三面角。截口三角形是逆時針繞向時，稱為正向三面角，否則稱為負向三面角。

相關分析

給定三面角S-ABC，倘若我們約定把SA，SB，SC依次叫做第一、第二、第三棱，那么便叫做有向三面角，記作。

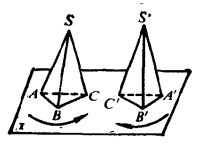
圖1

設以不通過頂點的任一平面π截三棱，從頂點S看π上的截口三角形，若圍線ABCA是逆時針方向(圖1左)，則稱有正向；如果是順時針方向(圖1右)，則稱有負向，轉向的正負與π的選擇無關。

倘若反向延長三面角S-ABC的三棱，得一新三面角S-A'B'C'(圖2)，稱為S-ABC的對頂三面角。若將SA與SA'，SB與SB'，SC與SC'相對應，那么顯見兩個三面角S-ABC和S-A'B'C'的對應的面角相等，對應的二面角相等；但它們的轉向相反。

圖2

兩個對頂三面角雖有對應相等的面角和二面角，在一般情況下卻是無法疊合的。因在一般情況下，S-ABC的三個面角不相等，所以S-A'B'C'中只有B'SC'面能和BSC面相疊合，因此，倘若兩個三面角能疊合，只有棱SA和SA'相疊合；同理SB須與SB'疊合，SC與SC'疊合，但這是不可能的：當SB’、SC'分別與SB、SC疊合以後，由於這兩個三面角有反向，棱SA且和SA'各在平面BSC的一側，決不可能疊合。

有向三面角的性質

有向三面角有以下性質：

(a)若互換三面角的兩棱，就改變了它的轉向，即和的向相反。

(b)若輪換三面角的三棱，它的向保持不變。即和及的向相同。

(c)假若三面角的前兩棱SA，SB分別重合於三面角的相應兩棱，則兩個三面角同屬於一類（有同一之向）或分屬於兩類（有相反之向），要看兩棱SC，SC'在平面ASB的同側或異側而定。

(d)兩三面角，不屬於同類（有相反之向）。

空間所有三面角的集，可以分作兩類具有性質(a)—(d)，而且只有一種分法。